题目内容
12.已知函数y=Asin(ωx+φ) (A>0,ω>0,0<φ<π)的最小正周期为$\frac{2π}{3}$,最小值为-2,图象过($\frac{5π}{9}$,0)(1)求该函数的解析式.
(2)求函数的单调区间.
分析 (1)由周期求的ω,由最值求得A,由特殊点的坐标求得φ的值,可得函数的解析式.
(2)利用正弦函数的单调性求得该函数的单调区间.
解答 解:(1)∵函数y=Asin(ωx+φ) (A>0,ω>0,)的最小正周期为$\frac{2π}{3}$,
∴$\frac{2π}{ω}$=$\frac{2π}{3}$,∴ω=3;∵函数y的最小值为-2,∴A=2;
根据函数的图象过($\frac{5π}{9}$,0),可得3•$\frac{5π}{9}$+φ=kπ,k∈Z,∴φ=$\frac{π}{3}$,
∴该函数的解析为y=2sin(3x+$\frac{π}{3}$).
(2)令2kπ-$\frac{π}{2}$≤3x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,求得$\frac{2kπ}{3}$-$\frac{5π}{18}$≤x≤$\frac{2kπ}{3}$+$\frac{π}{18}$,
可得函数的增区间为[$\frac{2kπ}{3}$-$\frac{5π}{18}$,$\frac{2kπ}{3}$+$\frac{π}{18}$],k∈Z.
令2kπ+$\frac{π}{2}$≤3x+$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,求得$\frac{2kπ}{3}$+$\frac{π}{18}$≤x≤$\frac{2kπ}{3}$+$\frac{7π}{18}$,
可得函数的增区间为[$\frac{2kπ}{3}$+$\frac{π}{18}$,$\frac{2kπ}{3}$+$\frac{7π}{18}$],k∈Z.
点评 本题主要考查正弦函数的图象,正弦函数的单调性,属于基础题.

练习册系列答案
相关题目
3.若质点P的运动方程为S(t)=2t2+t(S的单位为米,t的单位为秒),则当t=1时的瞬时速度为( )
| A. | 2米/秒 | B. | 3米/秒 | C. | 4米/秒 | D. | 5米/秒 |
7.若函数f(x)=$\left\{\begin{array}{l}{log_a}x,0<x≤1\\(4-a){x^2}-ax+1,x>1\end{array}$在(0,+∞)上单调递增,则实数a的取值范围是( )
| A. | (1,4) | B. | $[\frac{5}{2},4)$ | C. | $(1,\frac{5}{2}]$ | D. | $[\frac{5}{2},\frac{8}{3}]$ |
1.函数$f(x)=\frac{1}{{\sqrt{{x^2}-1}}}+lg({2+x})$的定义域是( )
| A. | (-2,-1) | B. | (-2,1) | C. | (-2,-1)∪(1,+∞) | D. | (-2,+∞) |
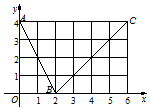 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(1)+f(3)=( )
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(1)+f(3)=( )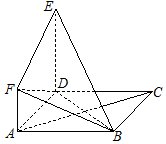 如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2.
如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2.