题目内容
14. 如图,在等腰梯形ABCD中,AB∥CD,AB<CD,AB=10,BC=3.
如图,在等腰梯形ABCD中,AB∥CD,AB<CD,AB=10,BC=3.(1)如果M为AB上一点,且满足∠DMC=∠A,求AM的长;
(2)如果点M在AB边上移动(点M与A,B不重合),且满足∠DMN=∠A,MN交BC延长线于N,设AM=x,CN=y,求y关于x的函数关系式,并写出x的取值范围.
分析 (1)构建图形,根据条件,利用△ADM∽△BMC,列出比例关系,求出答案;
(2)利用相似△ADM∽△BMN,得出相似比,根据题意得出函数表达式,结合(2)得出x的范围.
解答 解:(1)如图1,设AM的长为x,
∵AB∥CD,AD=BC,
∴∠A=∠B.
又∵∠A=∠DMC,∠1+∠2+∠A=∠2+∠DMC+∠3=180°,
∴∠1=∠3,∴△ADM∽△BMC.
∴$\frac{AM}{BC}=\frac{AD}{BM}$,即$\frac{x}{3}=\frac{3}{10-x}$,
解之得x1=1,x2=9,
经检验都是原分式方程的根.
∴AM=1或9….(6分)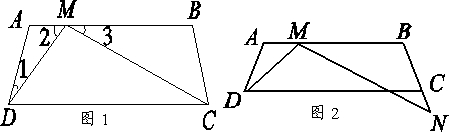
(2)由(1)可证得△ADM∽△BMN,
∴$\frac{AM}{BN}=\frac{AD}{BM}$,即$\frac{x}{y+3}=\frac{3}{10-x}$,
∴y=-$\frac{1}{3}$ x2+$\frac{10}{3}$ x-3,
所以y关于x的函数关系式为
y=-$\frac{1}{3}$ x2+$\frac{10}{3}$ x-3(1≤x≤9).….(12分)
点评 考察了函数的模型应用,难点是对题意的理解,把实际问题转换为函数问题.

练习册系列答案
相关题目
9.若一个命题的结论是“直线l在平面α内”,则用反证法证明这个命题时,第一步应作的假设为( )
| A. | 假设直线l∥平面α | B. | 假设直线l∩平面α于点A | ||
| C. | 假设直线l?平面α | D. | 假设直线l⊥平面α |
19.下列可以唯一确定一个平面的是( )
| A. | 一个四边形的4个顶点 | |
| B. | 过一个定点,且与两条异面直线垂直 | |
| C. | 过平面外一个定点,且与这个平面平行 | |
| D. | 过平面外一个定点,且与这个平面垂直 |
4.已知函数f(x)=2lnx+1在点(1,f(1))处的切线为l,点(an,an+1)在l上,且a1=2,则a2015=( )
| A. | 22014-1 | B. | 22014+1 | C. | 22015-1 | D. | 22015+1 |