题目内容
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=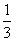 BB1,C1F=
BB1,C1F=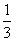 CC1.
CC1.
(1)求异面直线AE与A1 F所成角的大小;
(2)求平面AEF与平面ABC所成角的余弦值.

(1)建立如图所示的直角坐标系,则

 ,
, ,
, ,
, ,从而
,从而
 ,
, .
.
记 与
与 的夹角为
的夹角为 ,则有
,则有
 .
.
由异面直线 与
与 所成角的范围为
所成角的范围为 ,得异面直线
,得异面直线 与
与 所成角为60º.
所成角为60º.
(2)记平面 和平面
和平面 的法向量分别为n和m,则由题设可令
的法向量分别为n和m,则由题设可令 ,且有平面
,且有平面 的法向量为
的法向量为 ,
,  ,
, .
.
由 ,得
,得 ;由
;由 ,得
,得 .
.
所以 ,即
,即 .
.
记平面 与平面
与平面 所成的角为
所成的角为 ,
, .
.
由题意可知 为锐角,所以
为锐角,所以 .
.

练习册系列答案
相关题目
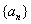 中,
中, 与
与 的等比中项为
的等比中项为 ,则
,则 的最小值为 .
的最小值为 . 对应的变换,再作N
对应的变换,再作N 对应的变换,得到的点的坐标为 (8,
对应的变换,得到的点的坐标为 (8, ),求实数a,b的值.
),求实数a,b的值. 满足
满足 ,且对于任意
,且对于任意 ,
, ,又
,又 ,则
,则 = .
= .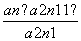 (n≥1,n∈N*),
(n≥1,n∈N*),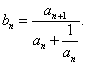
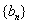 是常数列;
是常数列;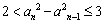 ;
; 的图像上各点的横坐标伸长到原的
的图像上各点的横坐标伸长到原的 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移 个单位,所得图像的一条对称轴方程为( )
个单位,所得图像的一条对称轴方程为( )  B.
B.  C.
C.  D.
D. 
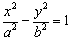 的左、右焦点分别为
的左、右焦点分别为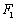 、
、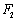 ,
,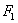 作圆
作圆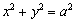 的切线分别交双曲线的左、右两支于
的切线分别交双曲线的左、右两支于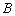 、
、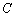 ,且
,且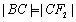 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )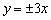 B.
B.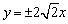
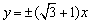 D.
D.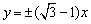

 B.
B. 
 D.
D. 
 ,B=
,B= ,则( )
,则( ) (B)
(B) (C)
(C) (D)
(D)