题目内容
3.在等比数列{an}中,已知a3=4,a7-2a5-32=0,则a7=64.分析 利用等比数列的通项公式即可得出.
解答 解:设等比数列{an}的公比为q,
∵a3=4,a7-2a5-32=0,
∴${a}_{1}{q}^{2}$=4,${a}_{1}{q}^{6}-2{a}_{1}{q}^{4}$=32.
解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{{q}^{2}=4}\end{array}\right.$,
∴${a}_{7}={a}_{1}{q}^{6}$=43=64.
故答案为:64.
点评 本题考查了等比数列的通项公式,属于基础题.

练习册系列答案
相关题目
18.已知函数g(x)=$\left\{\begin{array}{l}{\frac{1}{x+1}-3,-1<x≤0}\\{{x}^{2}-3x+2,0<x≤1}\end{array}\right.$,若方程g(x)-mx-m=0有且仅有两个不等的实根,则实数m的取值范围是( )
| A. | (-$\frac{9}{4}$,-2]∪[0,2] | B. | (-$\frac{11}{4}$,-2]∪[0,2] | C. | (-$\frac{9}{4}$,-2]∪[0,2) | D. | (-$\frac{11}{4}$,-2]∪[0,2) |
8.执行如图的程序框图,则输出S的值为( )


| A. | 2016 | B. | 2 | C. | $\frac{1}{2}$ | D. | -1 |
15.命题“?x∈R,tanx≠1”的否定是( )
| A. | ?x∉R,tanx≠1 | B. | ?x∈R,tanx=1 | C. | ?x∉R,tanx≠1 | D. | ?x∈R,tanx=1 |
11.已知直线l1:ax+2y+1=0,l2:(3-a)x-y+a=0,则条件“a=1”是“l1⊥l2“的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不必要也不充分条件 |
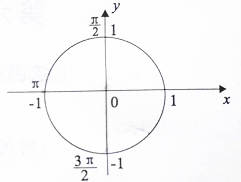 单位圆上三角函数值的集合解释是“角在弧上,值在线上”,试在图中画出α属于第Ⅲ象限的一个正弦值,余弦值.
单位圆上三角函数值的集合解释是“角在弧上,值在线上”,试在图中画出α属于第Ⅲ象限的一个正弦值,余弦值.