题目内容
设函数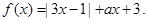
(Ⅰ)若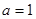 ,解不等式
,解不等式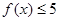 ;
;
(Ⅱ)若函数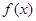 有最小值,求实数
有最小值,求实数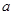 的取值范围.
的取值范围.
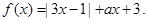
(Ⅰ)若
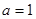 ,解不等式
,解不等式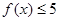 ;
;(Ⅱ)若函数
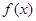 有最小值,求实数
有最小值,求实数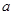 的取值范围.
的取值范围.(Ⅰ)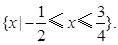 (Ⅱ)
(Ⅱ)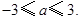
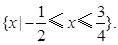 (Ⅱ)
(Ⅱ)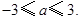
(Ⅰ)先化简不等式,然后利用绝对值不等式的解法求解;(Ⅱ)先化简函数,利用函数的单调性求解参数a的范围
(Ⅰ)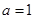 时,
时,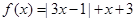 .
.
当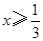 时,
时,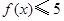 可化为
可化为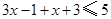 ,解之得
,解之得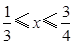 ;
;
当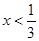 时,
时,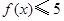 可化为
可化为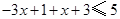 ,解之得
,解之得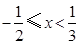 .
.
综上可得,原不等式的解集为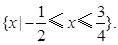 ……………5分
……………5分
(Ⅱ)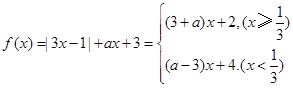
函数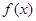 有最小值的充要条件为
有最小值的充要条件为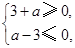 即
即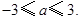
(Ⅰ)
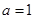 时,
时,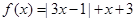 .
.当
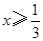 时,
时,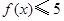 可化为
可化为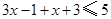 ,解之得
,解之得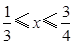 ;
;当
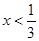 时,
时,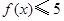 可化为
可化为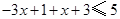 ,解之得
,解之得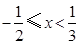 .
.综上可得,原不等式的解集为
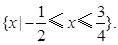 ……………5分
……………5分(Ⅱ)
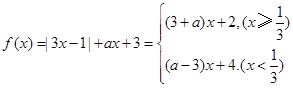
函数
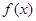 有最小值的充要条件为
有最小值的充要条件为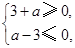 即
即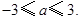

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 与
与
 与
与
 与
与
 与
与
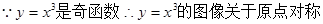 .”以上推理的大前提是_____________________.
.”以上推理的大前提是_____________________.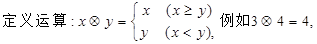 则下列等式不能成立的是( )
则下列等式不能成立的是( )


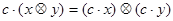 (其中
(其中 )
)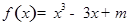 ,在
,在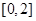 上任取三个数
上任取三个数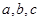 ,以
,以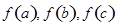 为边均可构成的三角形,则
为边均可构成的三角形,则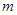 的范围是( )
的范围是( )

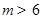

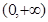 上为增函数的是( )
上为增函数的是( ) ;
; ;
; ;
; ;
;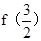 =_______________
=_______________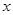 小时通过管道向所管辖区域供水
小时通过管道向所管辖区域供水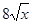 千吨.
千吨.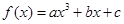 在
在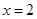 处取得极值为
处取得极值为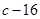
 有极大值28,求
有极大值28,求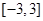 上的最大值.
上的最大值.