题目内容
已知函数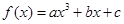 在
在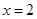 处取得极值为
处取得极值为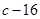
(1)求a、b的值;
(2)若 有极大值28,求
有极大值28,求 在
在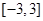 上的最大值.
上的最大值.
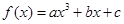 在
在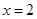 处取得极值为
处取得极值为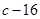
(1)求a、b的值;
(2)若
 有极大值28,求
有极大值28,求 在
在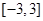 上的最大值.
上的最大值.(1) (2)
(2)
 (2)
(2)
(1)因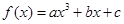 故
故 由于
由于 在点
在点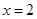 处取得极值
处取得极值
故有 即
即 ,化简得
,化简得 解得
解得
(2)由(1)知 ,
,
令 ,得
,得 当
当 时,
时, 故
故 在
在 上为增函数;
上为增函数;
当 时,
时, 故
故 在
在 上为减函数
上为减函数
当 时
时 ,故
,故 在
在 上为增函数。
上为增函数。
由此可知 在
在 处取得极大值
处取得极大值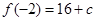 ,
, 在
在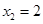 处取得极小值
处取得极小值 由题设条件知
由题设条件知 得
得 此时
此时 ,
, 因此
因此 上
上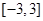 的最小值为
的最小值为
【考点定位】本题主要考查函数的导数与极值,最值之间的关系,属于导数的应用.(1)先对函数 进行求导,根据
进行求导,根据 =0,
=0, ,求出a,b的值.(1)根据函数
,求出a,b的值.(1)根据函数 =x3-3ax2+2bx在x=1处有极小值-1先求出函数中的参数a,b的值,再令导数等于0,求出极值点,判断极值点左右两侧导数的正负,当左正右负时有极大值,当左负右正时有极小值.再代入原函数求出极大值和极小值.(2)列表比较函数的极值与端点函数值的大小,端点函数值与极大值中最大的为函数的最大值,端点函数值与极小值中最小的为函数的最小值.
=x3-3ax2+2bx在x=1处有极小值-1先求出函数中的参数a,b的值,再令导数等于0,求出极值点,判断极值点左右两侧导数的正负,当左正右负时有极大值,当左负右正时有极小值.再代入原函数求出极大值和极小值.(2)列表比较函数的极值与端点函数值的大小,端点函数值与极大值中最大的为函数的最大值,端点函数值与极小值中最小的为函数的最小值.
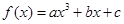 故
故 由于
由于 在点
在点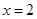 处取得极值
处取得极值故有
 即
即 ,化简得
,化简得 解得
解得
(2)由(1)知
 ,
,
令
 ,得
,得 当
当 时,
时, 故
故 在
在 上为增函数;
上为增函数;当
 时,
时, 故
故 在
在 上为减函数
上为减函数当
 时
时 ,故
,故 在
在 上为增函数。
上为增函数。由此可知
 在
在 处取得极大值
处取得极大值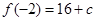 ,
, 在
在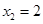 处取得极小值
处取得极小值 由题设条件知
由题设条件知 得
得 此时
此时 ,
, 因此
因此 上
上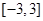 的最小值为
的最小值为
【考点定位】本题主要考查函数的导数与极值,最值之间的关系,属于导数的应用.(1)先对函数
 进行求导,根据
进行求导,根据 =0,
=0, ,求出a,b的值.(1)根据函数
,求出a,b的值.(1)根据函数 =x3-3ax2+2bx在x=1处有极小值-1先求出函数中的参数a,b的值,再令导数等于0,求出极值点,判断极值点左右两侧导数的正负,当左正右负时有极大值,当左负右正时有极小值.再代入原函数求出极大值和极小值.(2)列表比较函数的极值与端点函数值的大小,端点函数值与极大值中最大的为函数的最大值,端点函数值与极小值中最小的为函数的最小值.
=x3-3ax2+2bx在x=1处有极小值-1先求出函数中的参数a,b的值,再令导数等于0,求出极值点,判断极值点左右两侧导数的正负,当左正右负时有极大值,当左负右正时有极小值.再代入原函数求出极大值和极小值.(2)列表比较函数的极值与端点函数值的大小,端点函数值与极大值中最大的为函数的最大值,端点函数值与极小值中最小的为函数的最小值.
练习册系列答案
相关题目
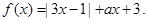
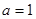 ,解不等式
,解不等式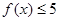 ;
;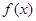 有最小值,求实数
有最小值,求实数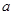 的取值范围.
的取值范围. 在[-1,2]上的最大值为4,最小值为m,且函数
在[-1,2]上的最大值为4,最小值为m,且函数 在
在 上是增函数,则a=____.
上是增函数,则a=____. 元(
元( )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为 元(
元( )时,一年的销售量为
)时,一年的销售量为 万件.
万件.
 与时间
与时间 的关系,可近似地表示为
的关系,可近似地表示为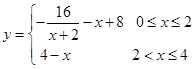 。只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用。
。只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用。 (m为常数),对任意
(m为常数),对任意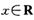 ,均有
,均有 恒成立.下列说法:
恒成立.下列说法: 为常数)的图象关于直线x=1对称,则b=1;
为常数)的图象关于直线x=1对称,则b=1;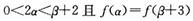 ,则必有
,则必有 ;
; 对任意X均有
对任意X均有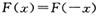 成立,且当
成立,且当 时,
时, ;又函数
;又函数 (c为常数),若存在
(c为常数),若存在 使得
使得 成立,则c的取值范围是(-1,13).其中说法正确的个数是
成立,则c的取值范围是(-1,13).其中说法正确的个数是  ,定义
,定义 ,其中,
,其中, ,则
,则 ( )
( )
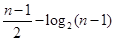


 的导函数为
的导函数为 ,且
,且 ,则
,则 .
.