题目内容

15．已知函数f（x）=ax3+bx2-1（a，b∈R，a≠0），若函数f（x）恰有两个零点x1，x2，则下列判断正确的是（　　）
A．当a＞0时，x1+x2＞0B．当a＞0时，x1•x2＞0C．当a＜0时，x1•x2＜0D．当a＜0时，x1+x2＜0

分析 求导f′（x）=3ax2+2bx=x（3ax+2b），从而可得f（-$\frac{2b}{3a}$）=0，f（0）=-1；从而作出函数的大致图象，从而解得．

解答 解：∵f（x）=ax3+bx2-1，
∴f′（x）=3ax2+2bx=x（3ax+2b），f（0）=-1；
又∵函数f（x）恰有两个零点x1，x2，
∴f（-$\frac{2b}{3a}$）=0，
当a＞0时，图象f（x）=ax3+bx2-1的大致形状如下，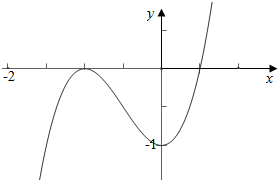

当a＜0时，图象f（x）=ax3+bx2-1的大大致形状如下，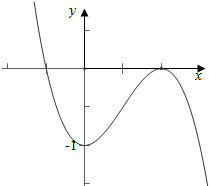

故x1•x2＜0，
故选：C．

点评 本题考查了导数的综合应用及数形结合的思想应用，属于中档题．

练习册系列答案
相关题目
5．设f（x）=$\left\{\begin{array}{l}{x-2，x≥10}\\{f（x+6），x＜10}\end{array}\right.$，则f（5）的值为9．
6．已知函数f（x）=x2+2ax+b，当a≥1时，若存在x0∈[-1，1]，使得|f（x0）|≥m对一切b∈R恒成立，则实数m的最大值为0．
3．已知曲线=2x2+3．
（1）求曲线在点P（1，5）处的切线方程；
（2）求曲线过点Q（2，9）的切线方程．
10．已知f（x）=2x2-（2a-1）x-1；
（1）若a＜1，判断f（x）在区间（$\frac{1}{4}$，+∞）的单调性并用定义证明；
（2）若f（x）在区间[-1，2]上不是单调函数，用集合表示实数a的取值范围．
20．己知二次函数f（x）满足f（x+1）-f（x）=2x+3．且f（0）=1
（1）求f（x）的解析式；
（2）在（1）的条件下．设g（x）=f（x）-kx．当x∈[-2，2]时．求g（x）最小值．
7．已知函数f（x）=$\frac{a{x}^{2}+1}{bx+c}$是奇函数，且f（1）=2，f（2）=$\frac{5}{2}$．
（1）求函数f（x）的表达式；
（2）当0＜x＜1时，用函数单调性的定义研究函数f（x）的单调性．
4．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{-2x}，x≤-1}\\{ax+3，x＞-1}\end{array}\right.$为单调函数，则实数a的取值范围是（　　）
A．（-1，0]B．[-1，0）C．（-1，0）D．（-∞，-1]
5．求下列各式的值：
（1）log3（27×92）；
（2）lg1002；
（3）lg0.00001；
（4）ln$\sqrt{e}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网