Question

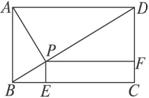
在矩形ABCD中，AB=5，BC=2，现截去一个角△PCQ，使P、Q分别落在边BC、CD上，且△PCQ的周长为8，设PC=x，CQ=y，则用x表示y的表达式为y=________．

Answer 1

，（0≤x≤2）
分析：由题意可得x+y+=8，平方化简可得解析式，注意x的取值范围．
解答：解：如图
由题意可得0≤x≤2，由勾股定理可得PQ=，
故△PCQ的周长=x+y+=8，即=8-x-y，
平方可得x²+y²=64+x²+y²-16x-16y+2xy，
整理可得32=8x+8y-xy，即（8-x）y=32-8x，
故y=，（0≤x≤2）
故答案为：，（0≤x≤2）
点评：本题考查函数解析式的求解，涉及完全平方公式，属基础题．