题目内容
如图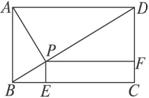
图
求证:AP3=BD·PE·PF.
证明:∵PE∥CD,∴△BEP∽△BCD.
∴![]() .∴PE=
.∴PE=![]() .
.
同理,由△BAP∽△DPF,
∴PF=![]() .
.
又∵AB=CD,∴PF=![]() .
.
又由射影定理得AP2=PB·PD,
∴BD·PE·PF=BD·![]() ·
·![]() =BP·PD·AP
=BP·PD·AP
=AP2·AP=AP3.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
如图
图
求证:AP3=BD·PE·PF.
证明:∵PE∥CD,∴△BEP∽△BCD.
∴![]() .∴PE=
.∴PE=![]() .
.
同理,由△BAP∽△DPF,
∴PF=![]() .
.
又∵AB=CD,∴PF=![]() .
.
又由射影定理得AP2=PB·PD,
∴BD·PE·PF=BD·![]() ·
·![]() =BP·PD·AP
=BP·PD·AP
=AP2·AP=AP3.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案