题目内容
设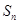 为等比数列
为等比数列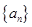 的前
的前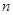 项和,已知
项和,已知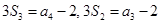 ,则公比
,则公比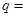 ( )
( )
| A.4 | B.3 | C.2 | D.8 |
A
解析试题分析:由于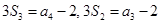 ,观察式子的特点,两式作差可知左边为
,观察式子的特点,两式作差可知左边为 ,因此得到关系式3a3=a4- a3,, 故有a4=4a3,则说明公比为4,那么选A.
,因此得到关系式3a3=a4- a3,, 故有a4=4a3,则说明公比为4,那么选A.
考点:本试题主要考查了等比数列的通项公式与前n项和关系的运用。
点评:解决该试题的关键是能够对于关系式采用整体的思想来作差处理,这是一种运算技巧,需要积累。

练习册系列答案
相关题目
在等比数列{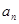 }中,若
}中,若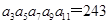 ,则
,则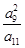 的值为
的值为
| A.9 | B.1 | C.2 | D.3 |
设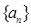 是各项为正数的无穷数列,
是各项为正数的无穷数列,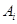 是边长为
是边长为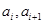 的矩形面积(
的矩形面积(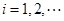 ),则
),则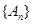 为等比数列的充要条件为
为等比数列的充要条件为
A.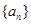 是等比数列。 是等比数列。 |
B.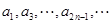 或 或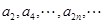 是等比数列。 是等比数列。 |
C.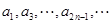 和 和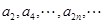 均是等比数列。 均是等比数列。 |
D.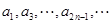 和 和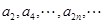 均是等比数列,且公比相同。 均是等比数列,且公比相同。 |
已知递增等比数列 满足
满足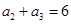 和
和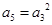 ,则
,则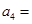
| A.1 | B.8 | C.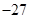 | D.8或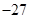 |
在数列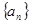 中,如果存在常数
中,如果存在常数
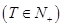 ,使得
,使得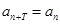 对于任意正整数
对于任意正整数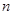 均成立,那么就称数列
均成立,那么就称数列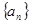 为周期数列,其中
为周期数列,其中 叫做数列
叫做数列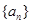 的周期. 已知数列
的周期. 已知数列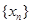 满足
满足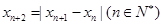 ,若
,若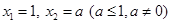 ,当数列
,当数列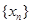 的周期为
的周期为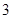 时,则数列
时,则数列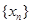 的前2012项的和
的前2012项的和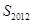 为 ( )
为 ( )
| A.1339 +a | B.1341+a | C.671 +a | D.672+a |
"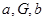 成等比"是"
成等比"是"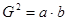 "的 条件( )
"的 条件( )
| A.充要条件 | B.充分不必要 | C.必要不充分 | D.既不充分也不必要 |
数列 满足
满足  ,其中
,其中 , 则这个数列的首项是( )
, 则这个数列的首项是( )
| A.1 | B.2 | C.3 | D.4 |
若数列{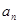 } 是公比为2的等比数列,且a 7 =" 16" ,则
} 是公比为2的等比数列,且a 7 =" 16" ,则 =( )
=( )
| A.1 | B.2 | C.4 | D.8 |
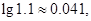
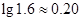 )
)