题目内容
设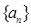 是各项为正数的无穷数列,
是各项为正数的无穷数列,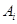 是边长为
是边长为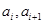 的矩形面积(
的矩形面积(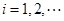 ),则
),则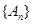 为等比数列的充要条件为
为等比数列的充要条件为
A.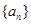 是等比数列。 是等比数列。 |
B.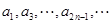 或 或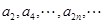 是等比数列。 是等比数列。 |
C.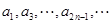 和 和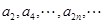 均是等比数列。 均是等比数列。 |
D.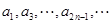 和 和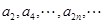 均是等比数列,且公比相同。 均是等比数列,且公比相同。 |
D
解析试题分析:依题意可知Ai=ai•ai+1,
∴Ai+1=ai+1•ai+2,
若{An}为等比数列则 =q(q为常数),则a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比均为q;
=q(q为常数),则a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比均为q;
反之要想{An}为等比数列则 需为常数,即需要a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比相等;
需为常数,即需要a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比相等;
故{An}为等比数列的充要条件是a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比相同.
故选D
考点:本题主要考查充要条件的概念,等比数列的概念。
点评:此类问题,要既考查充分性,又要考查必要性,已作出准确判断。

练习册系列答案
相关题目
公比为2的等比数列{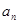 }的各项都是正数,且
}的各项都是正数,且
 =16,则
=16,则
A. | B. | C. | D. |
已知函数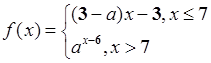 ,若数列
,若数列 满足
满足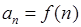 (
(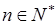 ),且
),且 是递增数列,则实数
是递增数列,则实数 的取值范围是( )
的取值范围是( )
A.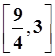 | B.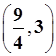 | C.(2,3) | D.(1,3) |
设 ,
,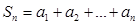 ,在
,在 中,正数的个数是( )
中,正数的个数是( )
| A.25 | B.50 | C.75 | D.100 |
已知等比数列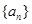 的公比为正数,且
的公比为正数,且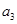
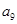 =2
=2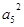 ,
,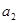 =1,则
=1,则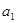 =( )
=( )
A.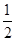 | B.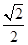 | C.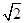 | D.2 |
若四个正数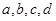 成等差数列,
成等差数列,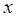 是
是 和
和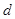 的等差中项,
的等差中项, 是
是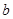 和
和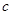 的等比中项,则
的等比中项,则 和
和 的大小关系是
的大小关系是
A.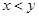 | B.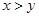 | C.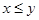 | D.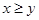 |
远望灯塔高七层,红光点点倍加增,只见顶层灯一盏,请问共有几盏灯?答曰:( )
| A.64 | B.128 | C.63 | D.127 |
设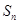 为等比数列
为等比数列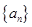 的前
的前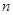 项和,已知
项和,已知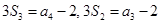 ,则公比
,则公比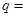 ( )
( )
| A.4 | B.3 | C.2 | D.8 |
在等比数列{an}中,a2=8,a5=64,,则公比q为 ( )
| A.2 | B.3 | C.4 | D.8 |