题目内容
一条直线l经过点P(3,2),且倾斜角是直线x-4y+3=0的倾斜角的2倍,
(1)求该直线的方程;
(2)求l与坐标轴围成的三角形的面积.
(1)求该直线的方程;
(2)求l与坐标轴围成的三角形的面积.
考点:正弦定理,直线的倾斜角
专题:解三角形
分析:(1)设所求直线倾斜角为θ,已知直线的倾斜角为α,则θ=2α,且tanα=
,利用倍角公式可得tanθ=tan2α=
.再利用点斜式即可得出.
(2)求出直线与坐标轴的交点,即可得出.
| 1 |
| 4 |
| 2tanα |
| 1-tan2α |
(2)求出直线与坐标轴的交点,即可得出.
解答:
解:(1)设所求直线倾斜角为θ,已知直线的倾斜角为α,则θ=2α,且tanα=
,
∴tanθ=tan2α=
=
=
,
从而方程为y-2=
(x-3),
化为8x-15y+6=0.
(2)直线方程为8x-15y+6=0,令y=0,得x=-
,令x=0,得y=
,
∴直线与x轴,y轴分别交于A(
,0),B(0,
),
∴S△AOB=
|OA||OB|=
×
×
=
.
| 1 |
| 4 |
∴tanθ=tan2α=
| 2tanα |
| 1-tan2α |
2×
| ||
1-(
|
| 8 |
| 15 |
从而方程为y-2=
| 8 |
| 15 |
化为8x-15y+6=0.
(2)直线方程为8x-15y+6=0,令y=0,得x=-
| 3 |
| 4 |
| 2 |
| 5 |
∴直线与x轴,y轴分别交于A(
| 3 |
| 4 |
| 2 |
| 5 |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 5 |
| 3 |
| 20 |
点评:本题考查了直线的点斜式、倍角公式、三角形的面积计算公式,属于基础题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
若a>b>0,则下列结论正确的是( )
| A、a2<b2 | ||
| B、ab<b2 | ||
C、a+b>2
| ||
| D、a-b>a+b |
已知集合A={x|x2-2x-3<0},B={x|log2x<2},则A∩B=( )
| A、(-1,4) |
| B、(-1,3) |
| C、(0,3) |
| D、(0,4) |
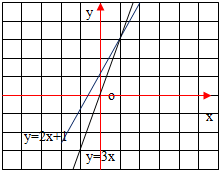 在同一坐标系中作出y=2x+1,y=3x的图象.
在同一坐标系中作出y=2x+1,y=3x的图象.