题目内容
对实数 和
和 ,定义运算“
,定义运算“ ”:
”: ,设函数
,设函数 ,若函数
,若函数 恰有两个不同的零点,则实数
恰有两个不同的零点,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C.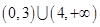 | D. |
A
解析试题分析:由题意知:
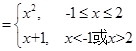 ,画出函数
,画出函数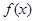 的图像,由图像可知;要使函数
的图像,由图像可知;要使函数 恰有两个不同的零点,
恰有两个不同的零点, 的范围为
的范围为 。
。
考点:函数的图像;函数的零点。
点评:函数的零点、对应方程的根、函数图像的交点,三者可以转化。本题就是把“函数 恰有两个不同的零点”转化为“函数
恰有两个不同的零点”转化为“函数
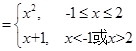 和函数
和函数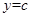 有两个不同的交点”来做的,体现了转化与化规的数学思想,以及数形结合的数学思想。
有两个不同的交点”来做的,体现了转化与化规的数学思想,以及数形结合的数学思想。

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
已知函数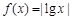 ,若
,若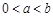 ,且
,且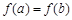 ,则
,则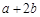 的取值范围是( )
的取值范围是( )
A.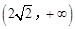 | B.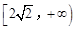 | C.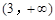 | D.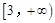 |
函数 在实数集上是增函数,则
在实数集上是增函数,则
A.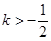 | B. | C. | D. |
在区间 上不是增函数的是( )
上不是增函数的是( )
A. | B. | C. | D. |
为了求函数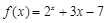 的一个零点,某同学利用计算器得到自变量
的一个零点,某同学利用计算器得到自变量 和函数
和函数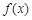 的部分对应值,如表所示:
的部分对应值,如表所示:
 | 1.25 | 1.3125 | 1.375 | 1.4375 | 1.5 | 1.5625 |
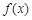 | -0.8716 | -0.5788 | -0.2813 | 0.2101 | 0.32843 | 0.64115 |
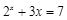 的近似解(精确到0.1)可取为
的近似解(精确到0.1)可取为(A)1.32 (B)1.39 (C)1.4 (D)1.3
函数 的零点所在的一个区间是
的零点所在的一个区间是
A. | B.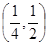 | C.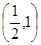 | D.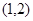 |
下列四组函数中表示同一函数的是( )
A. , , |
B. |
C. , , |
D. , ,  |
 的图象大致是 ( )
的图象大致是 ( )
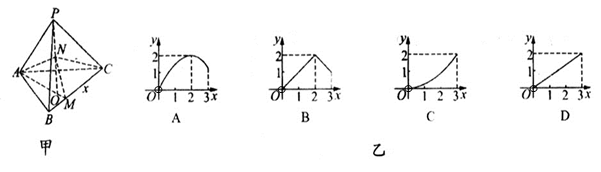
 的高
的高 ,
, ,
, ,M、N分别在
,M、N分别在 和
和 上,且
上,且 ,
, ,图乙中的四个图像大致描绘了三棱锥
,图乙中的四个图像大致描绘了三棱锥 的体积V与
的体积V与 的变化关系,其中正确的是( )
的变化关系,其中正确的是( )