题目内容
函数 的图象大致是 ( )
的图象大致是 ( )
D
解析试题分析:显然该函数是奇函数,奇函数的图象关于原点对称,所以排除A,B,当 时,
时, ,所以排除C.
,所以排除C.
考点:本小题主要考查根据函数的性质判断函数的图象,考查学生对图象的识别能力.
点评:由函数判断函数图象的问题时近几年高考中的热点问题,主要是根据定义域、单调性、奇偶性、最值等性质进行排除判断.

练习册系列答案
相关题目
在函数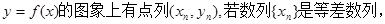 数列{
数列{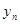 }是等比数列,则函数
}是等比数列,则函数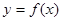 的解析式可能为( )
的解析式可能为( )
A.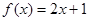 | B.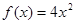 |
C.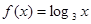 | D.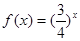 |
如果偶函数 ,当
,当 时,
时,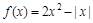 ,则
,则 在
在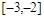 上是( )
上是( )
A.增函数,最大值为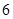 | B.增函数,最小值是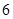 |
C.减函数,最大值为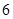 | D.减函数,最小值是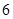 |
对实数 和
和 ,定义运算“
,定义运算“ ”:
”: ,设函数
,设函数 ,若函数
,若函数 恰有两个不同的零点,则实数
恰有两个不同的零点,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C.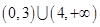 | D. |
已知函数 是奇函数,当
是奇函数,当 时,
时, ,则
,则 的值为
的值为
A. | B. | C. | D. |
下列函数中,与函数 相同的函数是 ( )
相同的函数是 ( )
A. | B. | C. | D. |
函数 的零点个数
的零点个数
| A.0 | B.1 |
| C.2 | D.1或2 |
下列函数是偶函数的是( )
A.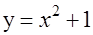 , ,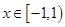 | B.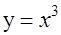 |
C. | D. |
函数 的定义域为 ( )
的定义域为 ( )
| A.(e,+∞) | B.[e,+∞) | C. (O,e] | D.(-∞,e] |