题目内容
【题目】在△ABC中，已知（a2+b2）sin（A﹣B）=（a2﹣b2）sin（A+B），则△ABC的形状（ ）
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
【答案】D
【解析】解：∵（a2+b2）（sinAcosB﹣cosAsinB）=（a2﹣b2）（sinAcosB+cosAsinB），
∴a2sinAcosB﹣a2cosAsinB+b2sinAcosB﹣b2cosAsinB=a2sinAcosB+a2cosAsinB﹣b2sinAcosB﹣b2cosAsinB，
整理得：a2cosAsinB=b2sinAcosB，
在△ABC中，由正弦定理 
= 
=2R得：a=2RsinA，b=2RsinB，代入整理得：
sinAcosA=sinBcosB，
∴2sinAcosA=2sinBcosB，
∴sin2A=sin2B，
∴2A=2B 或者2A=180°﹣2B，
∴A=B或者A+B=90°．
∴△ABC是等腰三角形或者直角三角形．
故选D．
练习册系列答案
相关题目
【题目】大学生赵敏利用寒假参加社会实践，对机械销售公司7月份至11月份销售某种机械配件的销售量及销售单价进行了调查，销售单价x元和销售量y件之间的一组数据如表所示：
月份 | 7 | 8 | 9 | 10 | 11 |
销售单价x元 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y件 | 11 | 10 | 8 | 6 | 5 |
（1）根据7至11月份的数据，求出y关于x的回归直线方程；
（2）预计在今后的销售中，销售量与销售单价仍然服从（1）中的关系，若该种机器配件的成本是2.5元/件，那么该配件的销售单价应定为多少元才能获得最大利润？ 参考公式：回归直线方程 
=b 
+a，其中b=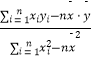 
．
参考数据： 
=392， 
=502.5．
