题目内容
设函数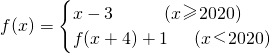 ,则f(2012)=________.
,则f(2012)=________.
2019
分析:题目给出的是分段函数,借助于递推式f(x)=f(x+4)+1把f(2012)转化到已知解析式的范围内,然后代入函数解析式求解.
解答:因为x<2020时,f(x)=f(x+4)+1,
所以f(2012)=f(2012+4)+1=f(2016)+1=f(2016+4)+1+1=f(2020)+2.
又当x≥2020时f(x)=x-3,所以f(2012)=f(2020)+2=(2020-3)+2=2019.
故答案为2019.
点评:本题考查了分段函数函数值的求法,分段函数分段处理,这是研究分段函数图象和性质最核心的理念,具体做法是:分段函数的定义域、值域是各段上x、y取值范围的并集,分段函数的奇偶性、单调性要在各段上分别论证;分段函数的最大值,是各段上最大值中的最大者,此题是基础题.
分析:题目给出的是分段函数,借助于递推式f(x)=f(x+4)+1把f(2012)转化到已知解析式的范围内,然后代入函数解析式求解.
解答:因为x<2020时,f(x)=f(x+4)+1,
所以f(2012)=f(2012+4)+1=f(2016)+1=f(2016+4)+1+1=f(2020)+2.
又当x≥2020时f(x)=x-3,所以f(2012)=f(2020)+2=(2020-3)+2=2019.
故答案为2019.
点评:本题考查了分段函数函数值的求法,分段函数分段处理,这是研究分段函数图象和性质最核心的理念,具体做法是:分段函数的定义域、值域是各段上x、y取值范围的并集,分段函数的奇偶性、单调性要在各段上分别论证;分段函数的最大值,是各段上最大值中的最大者,此题是基础题.

练习册系列答案
相关题目
 ,且当x∈(-3,-2)时,f(x)=5x,则f(201.2)=
,且当x∈(-3,-2)时,f(x)=5x,则f(201.2)=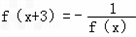 ,且当x∈(﹣3,﹣2)时,f(x)=5x,则f(201.2)=
,且当x∈(﹣3,﹣2)时,f(x)=5x,则f(201.2)=