题目内容
已知{an}是整数组成的数列,a1=1,且点(
,an+1)(n∈N*)在函数y=x2+2的图象上,则an=
| an |
2n-1
2n-1
.分析:由题意可得,an+1=an+2,结合等差数列的通项可求
解答:解:由题意可得,an+1=an+2
∴数列{an}是以1为首项,以2为公差的等差数列
an=1+2(n-1)=2n-1
故答案为:2n-1
∴数列{an}是以1为首项,以2为公差的等差数列
an=1+2(n-1)=2n-1
故答案为:2n-1
点评:本题主要考查了等差数列的通项公式的求解,属于基础试题

练习册系列答案
相关题目
 恒成立,求正整数m的最大值.
恒成立,求正整数m的最大值.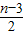 ,cn=
,cn=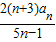 ,若对于任意的n∈N*,不等式
,若对于任意的n∈N*,不等式 -
-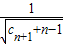 ≤0恒成立,求正整数m的最大值.
≤0恒成立,求正整数m的最大值.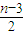 ,cn=
,cn= ,若对于任意的n∈N*,不等式
,若对于任意的n∈N*,不等式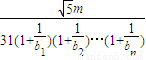 -
-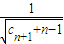 ≤0恒成立,求正整数m的最大值.
≤0恒成立,求正整数m的最大值.