Question

已知{a_n}是递增数列，其前n项和为S_n，a₁＞1，且10S_n=（2a_n+1）（a_n+2），n∈N^*．
（Ⅰ）求数列{a_n}的通项a_n；
（Ⅱ）是否存在m，n，k∈N^*，使得2（a_m+a_n）=a_k成立？若存在，写出一组符合条件的m，n，k的值；若不存在，请说明理由；
（Ⅲ）设b_n=a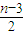_n-，c_n=，若对于任意的n∈N^*，不等式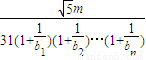-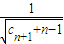≤0恒成立，求正整数m的最大值．

Answer 1

【答案】分析：（Ⅰ）令n=1代入10S_n=（2a_n+1）（a_n+2），求得a₁的值，根据，转化为等差数列，可以求得数列{a_n}的通项a_n；
（Ⅱ）假设存在m，n，k∈N^*，使得2（a_m+a_n）=a_k成立，代入数列{a_n}的通项a_n，经过分析得出矛盾，可以得到不存在m，n，k∈N^*，使得2（a_m+a_n）=a_k成立，
（Ⅲ）把数列{a_n}的通项a_n代入b_n=a_n-，c_n=，分离参数，转化为求某个数列的最值问题．
解答：解：（Ⅰ）∵10S_n=（2a_n+1）（a_n+3），
∴10a₁=（2a₁+1）（a₁+2），得2a₁²-5a₁+2=0，
解得a₁=2，或．
由于a₁＞1，所以a₁=2．
∵10S_n=（2a_n+1）（a_n+3），∴10S_n=2a_n²+5a_n+2．
故10a_n+1=10S_n+1-10S_n=2a_n+1²+5a_n+1+2-2a_n²-5a_n-2，
整理，得2（a_n+1²-a_n²）-5（a_n+1+a_n）=0，
即（a_n+1+a_n）[2（a_n+1-a_n）-5]=0．
因为{a_n}是递增数列，且a₁=2，故a_n+1+a_n≠0，
因此．
则数列{a_n}是以2为首项，为公差的等差数列．
所以．

（Ⅱ）满足条件的正整数m，n，k不存在，证明如下：
假设存在m，n，k∈N^*，使得2（a_m+a_n）=a_t，
则5m-1+5n-1=（5k-1）．
整理，得2m+2n-k=，①
显然，左边为整数，所以①式不成立．
故满足条件的正整数m，n，k不存在．

（Ⅲ）b_n=a_n-，
c_n=．
不等式≤0
可转化为
=
=．
设f（n）=，
则
=
=．
所以f（n+1）＞f（n），即当n增大时，f（n）也增大．
要使不等式
对于任意的n∈N^*恒成立，只需≤f（n）_min即可．
因为f（b）_min=f（1）=，所以，
即m≤．
所以，正整数m的最大值为8．
点评：此题是个难题．考查根据求数列通项公式，体现了分类讨论的思想．特别是（2）是个开放性的题目，解决策略一般假设存在，由假设出发，经过推理论证得到矛盾，（3）的设置，增加了题目的难度，对于恒成立问题，一般采取分离参数的方法，转化为求最值问题，体现 转化的思想．并根据数列的单调性求数列的最值．