题目内容
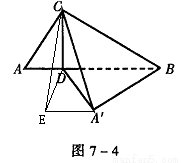
如图1-4-12,已知CD是Rt△ABC的斜边AB上的高线，求证:CD·AC=BC·AD.
图1-4-12
思路分析:分别在三个直角三角形Rt△ABC、Rt△ADC、Rt△BDC中运用射影定理，有CD2=BD·AD,BC2=BD·AB,AC2=AD·AB.将第一个式子和第三个式子相乘，就有CD2·AC2=BD·AB·AD2，将BD·AB换成BC2，然后两边开方即得.
证明：∵CD是Rt△ABC的斜边AB上的高线，
∴CD2=BD·AD,BC2=BD·AB,AC2=AD·AB.
∴CD2·AC2=BD·AB·AD2,CD·AC=BC·AD.
∴CD2·AC2=BC2·AD2.∴CD·AC=BC·AD.
练习册系列答案
优生乐园系列答案
相关题目
。
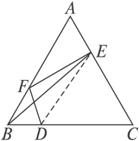
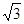