题目内容
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,过焦点做倾斜角为的120°的直线交
,过焦点做倾斜角为的120°的直线交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,
为坐标原点,![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过抛物线焦点,且与坐标轴不垂直的直线l交抛物线于![]() ,
,![]() 两点,
两点,![]() ,
,![]() 在抛物线上,且
在抛物线上,且![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() 四点都在圆
四点都在圆![]() 上,求圆
上,求圆![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)根据题意设直线方程为![]() ,联立方程,利用根与系数关系得
,联立方程,利用根与系数关系得![]() ,代入面积公式解得
,代入面积公式解得![]() ,进而求出抛物线的方程;
,进而求出抛物线的方程;
(2)由(1)可得焦点的坐标,设直线![]() 的方程为
的方程为![]() ,联立方程,表示出弦长
,联立方程,表示出弦长![]() ,得其中点
,得其中点![]() ,再由
,再由![]() ,
,![]() ,可知
,可知![]() 为线段
为线段![]() 的中垂线,设其方程为
的中垂线,设其方程为![]() ,再联立方程得弦长
,再联立方程得弦长![]() ,再设中点为
,再设中点为![]() ,再由
,再由![]() ,
,![]() ,
,![]() ,
,![]() 四点都在圆
四点都在圆![]() 上,等价于
上,等价于![]() ,从而
,从而![]() ,解方程解即可.
,解方程解即可.
(1)抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,
,
则过焦点倾斜角为120°的直线的方程为![]() ,
,
设![]() ,
,![]() ,
,
联立方程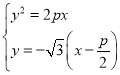 ,整理得
,整理得![]()
所以,![]() ,
,![]() ,
, ,
,
由![]() ,解得
,解得![]() .
.
故抛物线方程为![]() .
.
(2)由题意可设![]() 的方程为
的方程为![]() ,代入
,代入![]() 得
得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
故![]() 的中点为
的中点为![]() ,
,![]() .因为
.因为
![]() ,
,![]() ,故直线
,故直线![]() 为线段
为线段![]() 的垂直平分线,斜率为
的垂直平分线,斜率为![]() ,
,
设其为![]() ,则
,则![]() 方程为
方程为![]() ,
,
将上式代入![]() ,并整理得
,并整理得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
设![]() 中点为
中点为![]() ,故
,故![]() ,
,
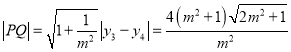 .
.
由于直线![]() 为线段
为线段![]() 的垂直平分线,故
的垂直平分线,故![]() ,
,![]() ,
,![]() ,
,![]() 四点在同一圆上等价于
四点在同一圆上等价于
![]() ,从而
,从而![]() ,
,
即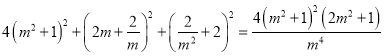 ,
,
化简得![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,圆心为
时,圆心为![]() ,
,![]() ,圆
,圆![]() 的方程为
的方程为![]() ;
;
当![]() 时,圆心为
时,圆心为![]() ,
,![]() ,圆
,圆![]() 的方程为
的方程为![]() .
.

【题目】某生鲜批发店每天从蔬菜生产基地以5元/千克购进某种绿色蔬菜,售价8元/千克,若每天下午4点以前所购进的绿色蔬菜没有售完,则对未售出的绿色蔬菜降价处理,以3元/千克出售.根据经验,降价后能够把剩余蔬菜全部处理完毕,且当天不再进货.该生鲜批发店整理了过往30天(每天下午4点以前)这种绿色蔬菜的日销售量(单位:千克)得到如下统计数据(视频率为概率)(注:x,y∈N*)
每天下午4点前销售量 | 350 | 400 | 450 | 500 | 550 |
天数 | 3 | 9 | x | y | 2 |
(1)求在未来3天中,至少有1天下午4点前的销售量不少于450千克的概率.
(2)若该生鲜批发店以当天利润期望值为决策依据,当购进450千克比购进500千克的利润期望值大时,求x的取值范围.
【题目】近年来,共享单车在我国各城市迅猛发展,为人们的出行提供了便利,但也给城市的交通管理带来了一些困难,为掌握共享单车在![]() 省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的
省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的![]() 指标
指标![]() 和
和![]() 指标
指标![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并说明
,并说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则认为
,则认为![]() 与
与![]() 具有较强的线性相关关系,否则认为没有较强的线性相关关系).
具有较强的线性相关关系,否则认为没有较强的线性相关关系).
(2)建立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标为7时,
指标为7时,![]() 指标的估计值.
指标的估计值.
(3)若某城市的共享单车![]() 指标
指标![]() 在区间
在区间![]() 的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至
的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至![]() 指标
指标![]() 在区间
在区间![]() 内现已知
内现已知![]() 省某城市共享单车的
省某城市共享单车的![]() 指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
参考公式:回归直线![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为
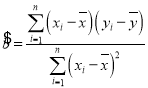 ,,
,,![]() 相关系数
相关系数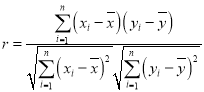
参考数据: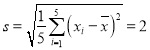 ,
,![]() ,
,![]() .
.