已知圆C的方程为(x-3)2+(y-4)2=22.平面上有A两点.点Q在圆C上.则△ABQ的面积的最大值是( )A．6B．3C．2D．1 题目和参考答案——青夏教育精英家教网——

题目内容

7．已知圆C的方程为（x-3）²+（y-4）²=2²，平面上有A（1，0），B（-1，0）两点，点Q在圆C上，则△ABQ的面积的最大值是（　　）

A．

6

B．

3

C．

2

D．

1

分析求出Q到AB的最大距离，即可求出△ABQ的面积的最大值．

解答解：由题意，Q到AB的最大距离为4+2=6，
∵|AB|=2，∴△ABQ的面积的最大值是$\frac{1}{2}×2×6$=6，
故选：A．

点评本题考查三角形面积的计算，考查圆的方程，比较基础．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

1．把函数y=sin（x-$\frac{π}{3}$）的图象向左平移$\frac{π}{6}$个单位长度，再将图象上所有点的横坐标缩短为原来的$\frac{1}{2}$倍（纵坐标不变）得到函数f（x）的图象．
（Ⅰ）写出函数f（x）的解析式；
（Ⅱ）若x∈[0，$\frac{5π}{6}$]时，关于x的方程f（x）-m=0有两个不等的实数根，求实数m的取值范围．

18．已知函数f（x）=sinωx+λcosωx，其图象的一个对称中心到最近的一条对称轴的距离为$\frac{π}{4}$，且在x=$\frac{π}{12}$处取得最大值．
（1）求λ的值．
（2）设$g（x）=af（x）+cos（4x-\frac{π}{3}）$在区间$（\frac{π}{4}，\frac{π}{3}）$上是增函数，求a的取值范围．

15．已知$\frac{a+2i}{i}$=b+i（a，b是实数），其中i是虚数单位，则ab=（　　）

2．已知函数f（x）=$\frac{x}{{e}^{x}}$（e是对自然对数的底数），则其导函数f'（x）=（　　）

$\frac{1+x}{{e}^{x}}$

$\frac{1-x}{{e}^{x}}$

12．已知实数x，y满足$\left\{\begin{array}{l}2x-y+4≥0\\ x-2y-5≤0\\ x+2y-4≤0\end{array}\right.$，则z=2x+3y的最大值与最小值之差为（　　）

-$\frac{68}{3}$

$\frac{371}{12}$

19．已知函数$f（x）=\sqrt{3}sinxcosx+sin（\frac{π}{4}+x）sin（\frac{π}{4}-x）$．
（ I）求函数f（x）对称轴方程和单调递增区间；
（ II）对任意$x∈[-\frac{π}{6}，\frac{π}{6}]$，f（x）-m≥0恒成立，求实数m的取值范围．

如图，矩形A_nB_nC_nD_n的一边A_nB_n在x轴上，另外两个顶点C_n，D_n在函数f（x）=x+$\frac{1}{2x}（{x＞0}）$的图象上．若点B_n的坐标为（n，0）（n∈N^*），记矩形A_nB_nC_nD_n的周长为a_n，则a₁+a₂+…+a₁₀（　　）

17．已知函数$f（x）=2sin（{ωx+φ}）（{ω＞0，-\frac{π}{2}＜φ＜\frac{π}{2}}）$的部分图象如图所示，则下列结论错误的是（　　）

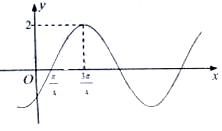
	A．	$φ=-\frac{π}{4}$
	B．	函数f（x）在$[{-\frac{π}{4}，\frac{3π}{4}}]$上单调递增
	C．	函数f（x）的一条对称轴是$x=\frac{3π}{4}$
	D．	为了得到函数f（x）的图象，只需将函数y=2cosx的图象向右平移$\frac{π}{4}$个单位