题目内容
如图,AB是圆O的直径,点C是圆O上不同于A,B的一点,点V是圆O所在平面外一点.
(Ⅰ) 若点E是AC的中点,求证:OE∥平面VBC;
(Ⅱ) 若VA=VB=VC,求证:VO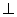 平面ABC.
平面ABC.
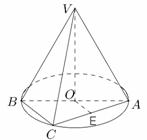
证明:
(Ⅰ) O,E分别是AB和AC的中点,
O,E分别是AB和AC的中点,

 OE∥BC .
OE∥BC .
又
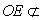 面VBC,
面VBC,  面VBC.
面VBC.
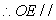 面VBC.
面VBC.
(Ⅱ) VA=VB,∵ △ABC为等腰三角形,
VA=VB,∵ △ABC为等腰三角形,
又 O为AB中点,∴ VO⊥AB;
O为AB中点,∴ VO⊥AB;
连接OC,在△VOA和△VOC中,OA =OC, VO=VO,VA=VC,
△VOA≌△VOC;-
∴ ∠V0A=∠VOC=90o. ∴ VO⊥OC;
 AB∩OC=O, AB
AB∩OC=O, AB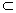 平面ABC, OC
平面ABC, OC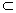 平面ABC,
平面ABC,
∴ VO⊥平面ABC.

练习册系列答案
相关题目
从某项综合能力测试中抽取50人的成绩,统计如下表,则这50人成绩的平
均数为__________,方差为__________.
| 分数 | 5 | 4 | 3 | 2 | 1 |
| 人数 | 10 | 5 | 15 | 15 | 5 |
(注:s2=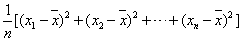 ,
,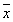 为数据
为数据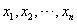 的平均数)
的平均数)
 为第三项,3为第六项的等比数列的公比,则
为第三项,3为第六项的等比数列的公比,则 ________.
________.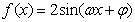
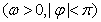 的部分图象如图所示,那么
的部分图象如图所示,那么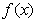 的表达式为
的表达式为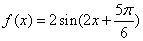 (B)
(B)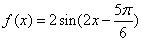
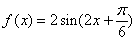 (D)
(D)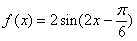

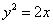 的准线方程是 ( )
的准线方程是 ( )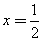 (B)
(B)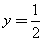 (C)
(C)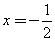 (D)
(D)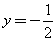
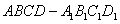 中,点
中,点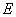 是棱
是棱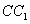 上的一个动点,平面
上的一个动点,平面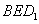 交棱
交棱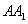 于点
于点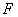 .则下列命题中假命题是 ( )
.则下列命题中假命题是 ( ) (A)存在点
(A)存在点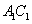 //平面
//平面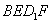
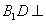 平面
平面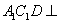 平面
平面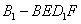 的体积均不变
的体积均不变 :
: 的左、右焦点分别为
的左、右焦点分别为 ,椭圆
,椭圆 满足
满足 . 若点
. 若点 是椭圆
是椭圆 的最大值为
的最大值为 B.
B.  C.
C.  D.
D. 
 中,点
中,点 ,
, ,若向量
,若向量 ,则实数
,则实数 _____.
_____.