题目内容
已知边长为
的正△ABC，点D，E分别在边AB，AC上，且DE∥BC，以DE为折痕，把△ADE折起至△A'DE，使点A'在平面BCED上的射影H始终落在BC边上，记
，则S的取值范围为 ．
【答案】分析：设△ADE的高为x，则DE到BC的距离为3-x，
，正三角形△ADE的边长AD=
，
=
=
，
，由此能求出S的取值范围．
解答：解：设△ADE的高为x，则DE到BC的距离为3-x，
，
正三角形△ADE的边长AD=
，
∴
=
=
，
，
6sx-9s=
，
，
∴
，或s≤0（舍）
故答案为：
．
点评：本题考查的是图形翻折变换的性质及平角的性质，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等的知识是解答此题的关键．
，正三角形△ADE的边长AD=，==，，由此能求出S的取值范围．解答：解：设△ADE的高为x，则DE到BC的距离为3-x，
，正三角形△ADE的边长AD=
，∴
==，，6sx-9s=
，，∴
，或s≤0（舍）故答案为：
．点评：本题考查的是图形翻折变换的性质及平角的性质，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等的知识是解答此题的关键．
练习册系列答案
巧学巧练系列答案
相关题目
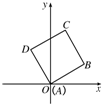已知边长为1的正方形ABCD中，AB与x轴正半轴成30°角．求点B和点D的坐标和