题目内容
设ξ~N(μ,δ2),且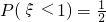 ,P(ξ>2)=p,则P(0<ξ<1)=
,P(ξ>2)=p,则P(0<ξ<1)=
- A.

- B.1-p
- C.
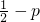
- D.1-2p
C
分析:由题意得随机变量ξ~N(1,δ2),再由正态分布图形可知图形关于x=1对称,故P(0<ξ<1)= (1-P(ξ>2)).
(1-P(ξ>2)).
解答:∵ξ~N(μ,δ2),且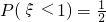 ,
,
∴μ=1,
由正态分布图形可知图形关于x=1对称,
故P(0<ξ<1)= (1-P(ξ>2))=
(1-P(ξ>2))= -P
-P
故选C.
点评:本题考查正态分布的概率问题,属基本题型的考查.解决正态分布的关键是抓好正态分布的图形特征.
分析:由题意得随机变量ξ~N(1,δ2),再由正态分布图形可知图形关于x=1对称,故P(0<ξ<1)=
 (1-P(ξ>2)).
(1-P(ξ>2)).解答:∵ξ~N(μ,δ2),且
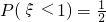 ,
,∴μ=1,
由正态分布图形可知图形关于x=1对称,
故P(0<ξ<1)=
 (1-P(ξ>2))=
(1-P(ξ>2))= -P
-P故选C.
点评:本题考查正态分布的概率问题,属基本题型的考查.解决正态分布的关键是抓好正态分布的图形特征.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目