题目内容
已知![]() 是过点
是过点![]() 的两条互相垂直的直线,且
的两条互相垂直的直线,且![]() 与双曲线
与双曲线![]() 各有两个交点,分别为A1、B1和A2、B2.
各有两个交点,分别为A1、B1和A2、B2.
(Ⅰ)求l1的斜率k1的取值范围;
(Ⅱ)若A1恰是双曲线的一个顶点,求│A2B2│的值.
解(Ⅰ)依照设,![]() 得斜率都存在,因为
得斜率都存在,因为![]() 过点
过点![]()
且与双曲线有两个交点,故方程组
 ①
①
有两个不同的解,在方程组①中消去![]() 整理得
整理得
![]() ②
②
若![]() 方程组①只有一个解,即
方程组①只有一个解,即![]() 与双曲线只有一个交点,与题设矛盾。故
与双曲线只有一个交点,与题设矛盾。故
![]() 即
即![]() 方程②的判别式为
方程②的判别式为
![]()
设![]() 的斜率为
的斜率为![]() 因为
因为![]() 过点
过点![]() 且与双曲线有两个交点,故方程组
且与双曲线有两个交点,故方程组
 ③
③
有两个不同的解,在方程组③中消去y, 整理得
![]()
同理有![]() ④
④
又因为l1⊥l2,所以有k1?k2=-1于是,l1、l2与双曲线各有两个交点,等价于
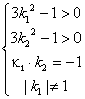
解得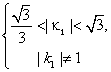
∴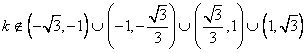
(Ⅱ)双曲线y2-x2=1的顶点为(0,1)、(0,-1).取A1(0,1)时,有
解得![]() 从而
从而![]()
将![]() 代人方程④得
代人方程④得
![]()
记l2与双曲线的两交点为A2(x1,y1)、B2(x2,y2),则
│A2B2│2 =(x1-x2)2+(y1-y2)2=3(x1-x2)2=3[(x1+x2)2-4x1x2].
由知![]()
∴![]()
即![]()
当取A1(0,-1)时,由双曲线y2-x2=1关于x轴的对称性,知
![]()
所以L1过双曲线的一个顶点时,![]()

练习册系列答案
相关题目
 、
、 是过点
是过点 的两条互相垂直的直线,且
的两条互相垂直的直线,且 、
、 与双曲线
与双曲线 各有两个交点,分别为
各有两个交点,分别为 、
、 和
和 、
、 ,求
,求 的取值范围.
的取值范围. :
: .
.
 (如图),直线
(如图),直线 分别与椭圆
分别与椭圆 两点,其中点
两点,其中点 满足
满足 ,且
,且 .
.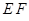 与
与 轴交点的位置与
轴交点的位置与 无关;
无关;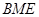 面积是∆
面积是∆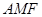 面积的5倍,求
面积的5倍,求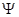 :
: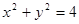 .
. 是过点
是过点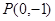 的两条互相垂直的直线,其中
的两条互相垂直的直线,其中 交圆
交圆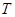 、
、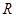 两点,
两点, 交椭圆
交椭圆 于另一点
于另一点 .求
.求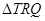 面积取最大值时直线
面积取最大值时直线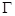 :
: .
.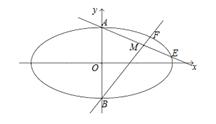
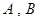 (如图),直线
(如图),直线 分别与椭圆
分别与椭圆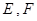 两点,其中点
两点,其中点 满足
满足 ,且
,且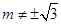 .
. 与
与 轴交点的位置与
轴交点的位置与 无关;
无关; 面积是∆
面积是∆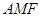 面积的5倍,求
面积的5倍,求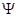 :
: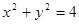 .
.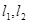 是过点
是过点 的两条互相垂直的直线,其中
的两条互相垂直的直线,其中 交圆
交圆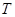 、
、 两点,
两点,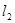 交椭圆
交椭圆 .求
.求 面积取最大值时直线
面积取最大值时直线