题目内容
已知![]() 是过点
是过点![]() 的两条互相垂直的直线,且
的两条互相垂直的直线,且![]() 与双曲线
与双曲线![]() 各两个交点,分别为
各两个交点,分别为![]() 和
和![]() .
.
(1)求![]() 的斜率
的斜率![]() 的取值范围; (2)若
的取值范围; (2)若![]() ,求
,求![]() 的方程.
的方程.
(1)
(2)![]() 时,
时,![]() :
:![]() :
:![]() ;
;
![]() 时,
时,![]() :
:![]() :
:![]()
解析:
(1)依题设,![]() 的斜率都存在,因为
的斜率都存在,因为![]() 过点
过点![]() 且与双曲线有两具交点,故方程组
且与双曲线有两具交点,故方程组
 ①
①
有两组不同实根,在方程①中消去![]() ,整理得
,整理得
![]() ②
②
若![]() ,则方程组①只有一个解,即
,则方程组①只有一个解,即![]() 与双曲线只有一个交点,与题设矛盾.故
与双曲线只有一个交点,与题设矛盾.故![]() 即
即![]() .方程②的判别式为
.方程②的判别式为
![]() .
.
设![]() 的斜率为
的斜率为![]() ,因为
,因为![]() 过点
过点![]() 且与双曲线有两个交点,故方程组
且与双曲线有两个交点,故方程组
 ③
③
有两个不同的解.在方程组③中消去![]() ,整理得
,整理得
![]() ④
④
类似前面的讨论,有![]() .
.
因为![]() ,所以
,所以![]() ,于是,
,于是,![]() 与双曲线各有两个交点,等价于下列混合组成立
与双曲线各有两个交点,等价于下列混合组成立
 ,解得
,解得 .
.
故 .
.
(2)设![]() ,则(1)的解答中方程②知
,则(1)的解答中方程②知
![]()
所以![]()
![]() ⑤
⑤
同理可得![]() ⑥
⑥
由![]() ,得
,得![]() .
.
将⑤,⑥代入上式得![]() ,
,
解得 ![]() .
.
取![]() 时,
时,![]() :
:![]() :
:![]() ;
;
即![]() 时,
时,![]() :
:![]() :
:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 、
、 是过点
是过点 的两条互相垂直的直线,且
的两条互相垂直的直线,且 、
、 与双曲线
与双曲线 各有两个交点,分别为
各有两个交点,分别为 、
、 和
和 、
、 ,求
,求 的取值范围.
的取值范围.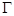 :
: .
.
 (如图),直线
(如图),直线 分别与椭圆
分别与椭圆 两点,其中点
两点,其中点 满足
满足 ,且
,且 .
.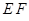 与
与 轴交点的位置与
轴交点的位置与 无关;
无关;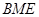 面积是∆
面积是∆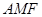 面积的5倍,求
面积的5倍,求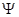 :
: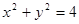 .
. 是过点
是过点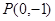 的两条互相垂直的直线,其中
的两条互相垂直的直线,其中 交圆
交圆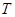 、
、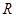 两点,
两点, 交椭圆
交椭圆 于另一点
于另一点 .求
.求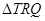 面积取最大值时直线
面积取最大值时直线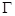 :
: .
.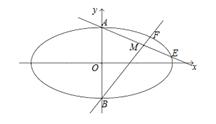
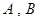 (如图),直线
(如图),直线 分别与椭圆
分别与椭圆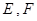 两点,其中点
两点,其中点 满足
满足 ,且
,且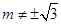 .
. 与
与 轴交点的位置与
轴交点的位置与 无关;
无关; 面积是∆
面积是∆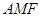 面积的5倍,求
面积的5倍,求 :
: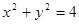 .
.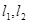 是过点
是过点 的两条互相垂直的直线,其中
的两条互相垂直的直线,其中 交圆
交圆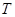 、
、 两点,
两点,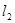 交椭圆
交椭圆 .求
.求 面积取最大值时直线
面积取最大值时直线