题目内容
已知函数![]()
(1)求函数![]() 的导函数
的导函数![]() ;
;
(2)当![]() 时,若函数
时,若函数![]() 是R上的增函数,求
是R上的增函数,求![]() 的最小值;
的最小值;
(3)当![]() 时,函数
时,函数![]() 在
在![]() 上存在单调递增区间,求m的取值范围。
上存在单调递增区间,求m的取值范围。
Ⅰ)解:![]() .
.  (Ⅱ)因为函数
(Ⅱ)因为函数![]() 是
是![]() 上的增函数,所以
上的增函数,所以![]() 在
在![]() 上恒成立.
上恒成立.
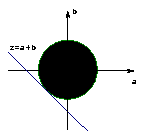
则有![]() ,即
,即![]() .
.
可用圆面的几何意义解得
![]() 的最小值
的最小值![]() (Ⅲ)①当
(Ⅲ)①当![]() 时,
时,![]() 是开口向上的抛物线,显然
是开口向上的抛物线,显然![]() 在
在![]() 上存在子区间使得
上存在子区间使得![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .②当
.②当![]() 时,显然成立.
时,显然成立.
③当![]() 时,
时,![]() 是开口向下的抛物线,要使
是开口向下的抛物线,要使![]() 在
在![]() 上存在子区间使
上存在子区间使![]() ,应满足
,应满足 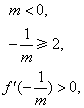 或
或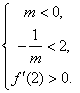
![]() 解得
解得![]() ,或
,或![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.
则![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
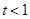 时,求函数
时,求函数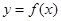 的单调区间;
的单调区间;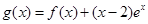 ,试问函数
,试问函数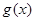 在
在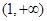 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
 的定义域;
的定义域; 为何值时,函数值大于1.
为何值时,函数值大于1.
 ,
, ,
, ,
, 这几个函数值,你能发现f(x)与
这几个函数值,你能发现f(x)与 有什么关系?并证明你的结论;
有什么关系?并证明你的结论;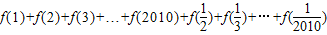 的值;
的值; 在区间(0,+∞)上的单调性.
在区间(0,+∞)上的单调性.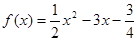
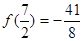 ,求
,求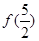
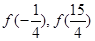 的大小
的大小