题目内容
已知函数
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)求函数 的极值.
的极值.
(1) ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)根据导数的几何意义,当 时,
时, ,得出
,得出 ,再代入点斜式直线方程;
,再代入点斜式直线方程;
(2) 讨论,当
讨论,当 和
和 两种情况下的极值情况.
两种情况下的极值情况.
试题解析:解:函数 的定义域为
的定义域为 ,
, .
.
(1)当 时,
时, ,
, ,
,  ,
,  在点
在点 处的切线方程为
处的切线方程为 ,
,
即 .
.
(2)由 可知:
可知:
①当 时,
时, ,函数
,函数 为
为 上的增函数,函数
上的增函数,函数 无极值;
无极值;
②当 时,由
时,由 ,解得
,解得 ;
;  时,
时, ,
, 时,
时,
 在
在 处取得极小值,且极小值为
处取得极小值,且极小值为 ,无极大值.
,无极大值.
综上:当 时,函数
时,函数 无极值
无极值
当 时,函数
时,函数 在
在 处取得极小值
处取得极小值 ,无极大值.
,无极大值.
考点:1.导数的几何意义;2.利用导数求极值.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
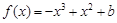 ,
,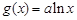 .
.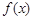 的极大值为
的极大值为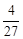 ,求实数
,求实数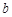 的值;
的值;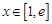 ,都有
,都有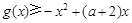 恒成立,求实数
恒成立,求实数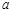 的取值范围;
的取值范围;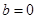 ,若
,若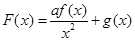 关于实数a 可线性分解,求
关于实数a 可线性分解,求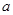 取值范围.
取值范围.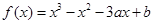 .
.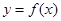 在点
在点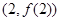 处与直线
处与直线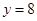 相切,求a,b的值;
相切,求a,b的值; 的单调区间.
的单调区间.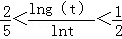 .
.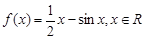 .
. 的递减区间;
的递减区间;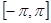 上的最值.
上的最值. ,曲线
,曲线 经过点
经过点 ,
, 处的切线为
处的切线为 .
. 、
、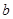 的值;
的值; ,使得
,使得 时,
时, 恒成立,求
恒成立,求 ,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).