题目内容
10．函数f（x）=$\frac{2x+1}{x-1}$，x∈[-1，1）U（1，3]的值域为（-∞，$\frac{1}{2}$]∪[$\frac{7}{2}，+$∞）．分析 把函数解析式变形，然后画出图形，数形结合求得函数值域．
解答 解：f（x）=$\frac{2x+1}{x-1}$=$\frac{2（x-1）+3}{x-1}=\frac{3}{x-1}+2$，
作出函数特性如图，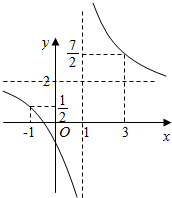
由图可知，函数f（x）=$\frac{2x+1}{x-1}$，x∈[-1，1）U（1，3]的值域为（-∞，$\frac{1}{2}$]∪[$\frac{7}{2}，+$∞）．
故答案为：（-∞，$\frac{1}{2}$]∪[$\frac{7}{2}，+$∞）．
点评 本题考查函数的值域及其求法，考查了数形结合的解题思想方法，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
20．已知函数f（x）=log4（4x+1）+kx（k∈R）是偶函数．
（1）求k的值；
（2）设g（x）=log4（a•2x-1），若函数f（x）与g（x）的图象有且只有一个公共点，求实数a的取值范围．
（1）求k的值；
（2）设g（x）=log4（a•2x-1），若函数f（x）与g（x）的图象有且只有一个公共点，求实数a的取值范围．
18．已知函数y=f（x）是奇函数，当x＞0时，f（x）=2x-1，则f（f（f（-3）））的值等于（ ）
| A． | $\frac{1}{17}$ | B． | -$\frac{1}{17}$ | C． | 17 | D． | -17 |