题目内容
(本题满分12分)已知函数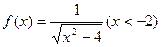 .(Ⅰ) 求f –1(x);(Ⅱ) 若数列{an}的首项为a1=1,
.(Ⅰ) 求f –1(x);(Ⅱ) 若数列{an}的首项为a1=1,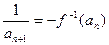 (nÎN+),求{an}的通项公式an;(Ⅲ) 设bn=an+12+an+22+¼+a2n+12,是否存在最小的正整数k,使对于任意nÎN+有bn<
(nÎN+),求{an}的通项公式an;(Ⅲ) 设bn=an+12+an+22+¼+a2n+12,是否存在最小的正整数k,使对于任意nÎN+有bn<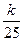 成立.若存在,求出k的值;若不存在,说明理由.
成立.若存在,求出k的值;若不存在,说明理由.
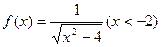 .(Ⅰ) 求f –1(x);(Ⅱ) 若数列{an}的首项为a1=1,
.(Ⅰ) 求f –1(x);(Ⅱ) 若数列{an}的首项为a1=1,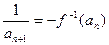 (nÎN+),求{an}的通项公式an;(Ⅲ) 设bn=an+12+an+22+¼+a2n+12,是否存在最小的正整数k,使对于任意nÎN+有bn<
(nÎN+),求{an}的通项公式an;(Ⅲ) 设bn=an+12+an+22+¼+a2n+12,是否存在最小的正整数k,使对于任意nÎN+有bn<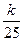 成立.若存在,求出k的值;若不存在,说明理由.
成立.若存在,求出k的值;若不存在,说明理由.(Ⅰ)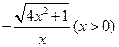 (Ⅱ)
(Ⅱ)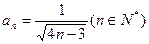
(Ⅲ)kmin=8,即存在最小的正整数k=8,使得
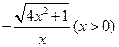 (Ⅱ)
(Ⅱ)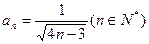
(Ⅲ)kmin=8,即存在最小的正整数k=8,使得

(Ⅰ)∵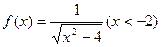 ,∴
,∴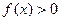 ,由y=
,由y=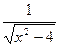 解得:
解得: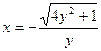 ,∴
,∴
(Ⅱ)由题意得: ,∴
,∴
∴{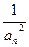 }是以
}是以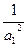 =1为首项,以4为公差的等差数列.∴
=1为首项,以4为公差的等差数列.∴ ,∴
,∴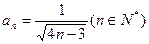 .
.
(Ⅲ)∴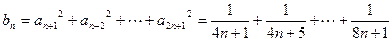
则 ,∴
,∴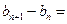
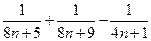
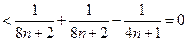 ,∴
,∴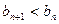 ,∴ {bn}是一单调递减数列.∴
,∴ {bn}是一单调递减数列.∴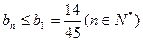 ,要使
,要使 ,则
,则 ,∴
,∴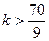 ,又kÎN* ,∴k³8 ,∴kmin=8,即存在最小的正整数k=8,使得
,又kÎN* ,∴k³8 ,∴kmin=8,即存在最小的正整数k=8,使得
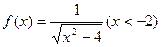 ,∴
,∴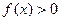 ,由y=
,由y=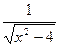 解得:
解得: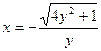 ,∴
,∴
(Ⅱ)由题意得:
 ,∴
,∴
∴{
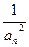 }是以
}是以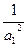 =1为首项,以4为公差的等差数列.∴
=1为首项,以4为公差的等差数列.∴ ,∴
,∴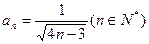 .
. (Ⅲ)∴
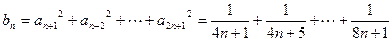
则
 ,∴
,∴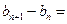
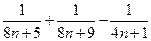
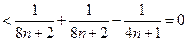 ,∴
,∴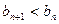 ,∴ {bn}是一单调递减数列.∴
,∴ {bn}是一单调递减数列.∴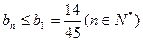 ,要使
,要使 ,则
,则 ,∴
,∴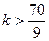 ,又kÎN* ,∴k³8 ,∴kmin=8,即存在最小的正整数k=8,使得
,又kÎN* ,∴k³8 ,∴kmin=8,即存在最小的正整数k=8,使得

练习册系列答案
相关题目
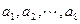 为各项都是正数的等差数列,公差
为各项都是正数的等差数列,公差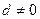 ,则( )
,则( )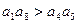
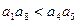
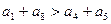
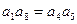
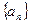 :
: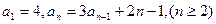 ,求
,求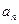 .
.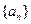 满足:
满足: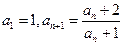
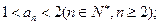
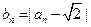
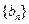 是递减数列;(2)设
是递减数列;(2)设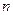 项和为
项和为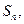 求证:
求证: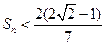
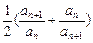 (n∈N*),求
(n∈N*),求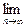 (b1+b2+b3+…+bn-n).
(b1+b2+b3+…+bn-n).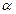 为锐角,且
为锐角,且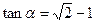 ,
,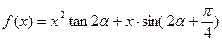 ,数列{an}的首项
,数列{an}的首项 .
.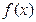 的表达式;
的表达式;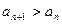 ;
; 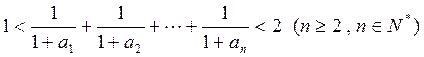
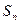 为等差数列
为等差数列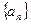 的前
的前 项和,
项和,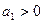 ,
, ,问数列的前几项和最大?
,问数列的前几项和最大? ,
,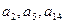 成等比数列,求数列
成等比数列,求数列