题目内容
已知△ABC的三个内角A、B、C所对的三边分别是a、b、c,平面向量 ,平面向量
,平面向量 .
.
(I)如果 ,求a的值;
,求a的值;
(II)若 ,请判断△ABC的形状.
,请判断△ABC的形状.
解:(I)由余弦定理及已知条件得a2+b2-ab=4,
∵ ,
,
∴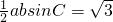 .
.
∴ab=4.
联立方程组得 .
.
∴a=2.
(II)∵ ,∴sinC-sin2A+sin(B-A)=0.
,∴sinC-sin2A+sin(B-A)=0.
化简得cosA(sinB-sinA)=0.
∴csoA=0或sinB-sinA=0.
当 ,
,
此时△ABC是直角三角形;
当sinB-sinA=0时,即sinB=sinA,
由正弦定理得b=a,
此时△ABC为等腰三角形.
∴△ABC是直角三角形或等腰三角形.
分析:(I)根据余弦定理以及c和C的值可求得a2+b2-ab=4,进而根据三角形面积公式求得ab的值,最后联立方程求得a.
(II)根据) 可推断出sinC-sin2Asin(B-A)=0.化简整理求得A为90°判断出三角形为直角三角形或A=B判断三角形为等腰三角形.
可推断出sinC-sin2Asin(B-A)=0.化简整理求得A为90°判断出三角形为直角三角形或A=B判断三角形为等腰三角形.
点评:本题主要考查了余弦定理的应用,三角形形状的判断,平面向量的性质等.考查了学生综合运用所学知识解决问题的能力.
∵
 ,
,∴
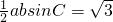 .
.∴ab=4.
联立方程组得
 .
.∴a=2.
(II)∵
 ,∴sinC-sin2A+sin(B-A)=0.
,∴sinC-sin2A+sin(B-A)=0.化简得cosA(sinB-sinA)=0.
∴csoA=0或sinB-sinA=0.
当
 ,
,此时△ABC是直角三角形;
当sinB-sinA=0时,即sinB=sinA,
由正弦定理得b=a,
此时△ABC为等腰三角形.
∴△ABC是直角三角形或等腰三角形.
分析:(I)根据余弦定理以及c和C的值可求得a2+b2-ab=4,进而根据三角形面积公式求得ab的值,最后联立方程求得a.
(II)根据)
 可推断出sinC-sin2Asin(B-A)=0.化简整理求得A为90°判断出三角形为直角三角形或A=B判断三角形为等腰三角形.
可推断出sinC-sin2Asin(B-A)=0.化简整理求得A为90°判断出三角形为直角三角形或A=B判断三角形为等腰三角形.点评:本题主要考查了余弦定理的应用,三角形形状的判断,平面向量的性质等.考查了学生综合运用所学知识解决问题的能力.

练习册系列答案
相关题目