题目内容
【题目】已知椭圆![]() 经过点
经过点![]() ,离心率
,离心率![]() .
.
(1)求![]() 的方程;
的方程;
(2)设直线![]() 经过点
经过点![]() 且与
且与![]() 相交于
相交于![]() 两点(异于点
两点(异于点![]() ),记直线
),记直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,证明:
,证明: ![]() 为定值.
为定值.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】【试题分析】(1)依题意可知![]() ,解方程组可求得椭圆的标准方程.(2)当直线斜率
,解方程组可求得椭圆的标准方程.(2)当直线斜率![]() 斜率不存在时,不符合题意.当斜率存在时,设出直线的方程,联立直线的方程和椭圆的方程,写出韦达定理,计算
斜率不存在时,不符合题意.当斜率存在时,设出直线的方程,联立直线的方程和椭圆的方程,写出韦达定理,计算![]() 的值,化简后结果为
的值,化简后结果为![]() ,由此证明结论成立.
,由此证明结论成立.
【试题解析】
(1)因为椭圆![]() ,经过点
,经过点![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() ,解得
,解得![]() .
.
故而可得椭圆的标准方程为: ![]() .
.
(2)若直线![]() 的斜率不存在,则直线
的斜率不存在,则直线![]() 的方程为
的方程为![]() ,
,
此时直线与椭圆相切,不符合题意.
设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
联立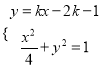 ,得
,得![]() .
.
设![]() ,
, ![]() ,则
,则
![]()
![]()
![]()
![]()
![]()
![]()
所以![]() 为定值,且定值为-1.
为定值,且定值为-1.

练习册系列答案
相关题目
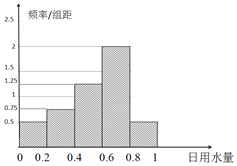
【题目】为达到节水节电的目的,某家庭记录了20天的日用电量xi(单位:度)的频数分布表和这20天相应的日用水量yi(单位:m3)的频率分布直方图如下:
日用电量xi | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) |
频数(天) | 2 | 5 | 7 | 3 | 3 |
(1)假设水费为2.5元/m3,电费为0.6元/度,用以上数据估计该家庭日用电量的平均值和日用水量的平均值,并据此估计该家庭一个月的水费和电费一共是多少?(一个月按30天算,同一组中的数据以这组数据所在区间中点的值作代表);
(2)假设该家庭的日用水量y和日用电量x可用线性回归模型来拟合,请利用(1)中的计算数据及所给的参考数据和公式,建立y与x的回归方程,预测若该家庭日用电量为20度时的日用水量是多少m3?(回归方程的系数小数点后保留2位小数)
参考数据:![]() xiyi=65,
xiyi=65,![]() 612
612
参考公式:回归方程![]() x
x![]() 中斜率和截距的公式分别为:
中斜率和截距的公式分别为:
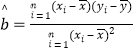 ,
,![]()