题目内容
(本小题满分12分)设函数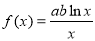 ,
,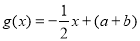 (其中
(其中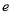 为自然对数的底数,
为自然对数的底数,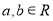 且
且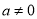 ),曲线
),曲线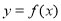 在点
在点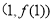 处的切线方程为
处的切线方程为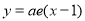 .
.
(1)求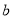 的值;
的值;
(2)若对任意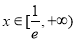 ,
,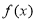 与
与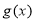 有且只有两个交点,求
有且只有两个交点,求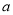 的取值范围.
的取值范围.
(1) ;(2)实数
;(2)实数 的取值范围为
的取值范围为 .
.
【解析】
试题分析:(1)求导 ,从而可得
,从而可得 ,从而解得;
,从而解得;
(2) ,则任意
,则任意 ,
, 与
与 有且只有两个交点,等价于函数
有且只有两个交点,等价于函数 在
在 有且只有两个零点,求导
有且只有两个零点,求导 ,从而分类讨论求
,从而分类讨论求 的取值范围.
的取值范围.
试题解析:(1)由 ,得
,得 , 1分
, 1分
由题意得 , 2分 ∵
, 2分 ∵ ,∴
,∴ ; 3分
; 3分
(2)令 ,则任意
,则任意 ,
, 与
与 有且只有两个交点,等价于函数
有且只有两个交点,等价于函数 在
在 有且只有两个零点,由
有且只有两个零点,由 ,得
,得 , 5分
, 5分
①当 时,由
时,由 得
得 ,由
,由 得
得 ,
,
此时 在
在 上单调递减,在
上单调递减,在 上单调递增,∵
上单调递增,∵ ,
,
 ,(或当
,(或当 时,
时, 亦可),∴要使得
亦可),∴要使得 在
在 上有且只有两个零点,则只需
上有且只有两个零点,则只需
 ,即
,即 , 7分
, 7分
②当 时,由
时,由 得
得 或
或 ,由
,由 得
得 ,此时
,此时 在
在 上单调递减,在
上单调递减,在 和
和 上单调递增. 此时
上单调递增. 此时 ,∴此时
,∴此时 在
在 至多只有一个零点,不合题意, 9分
至多只有一个零点,不合题意, 9分
③当 时,由
时,由 得
得 或
或 ,由
,由 得
得 ,此时
,此时 在
在 和
和 上单调递增,在
上单调递增,在 上单调递减,且
上单调递减,且 ,∴
,∴ 在
在 至多只有一个零点,不合题意, 11分
至多只有一个零点,不合题意, 11分
综上所述, 的取值范围为
的取值范围为 ; 12分
; 12分
考点:导数的运用.

练习册系列答案
相关题目
 处的切线l与直线
处的切线l与直线 垂直,函数
垂直,函数
 的值;
的值; 存在单调递减区间,求实数
存在单调递减区间,求实数 的取值范围;
的取值范围; 是函数
是函数 的两个极值点,若
的两个极值点,若 ,求
,求 的最小值。
的最小值。 的总体抽取容量为
的总体抽取容量为 的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同的方法抽取样本时,总体中每个个体被抽中的概率分别为
的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同的方法抽取样本时,总体中每个个体被抽中的概率分别为 ,则 ( )
,则 ( ) B.
B.
 D.
D.
 满足
满足 ,且
,且 的最大值为10,则
的最大值为10,则 的值为( )
的值为( ) ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 中,三内角
中,三内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 ,
, ,
, 为
为 是
是 是圆
是圆 上一动点,当
上一动点,当 取得最大值时,
取得最大值时, 的最大值为_______.
的最大值为_______.

 B.
B. C.
C. D.
D.
 ,则函数
,则函数 在区间
在区间 上的值域是 .
上的值域是 .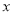 轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是
轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是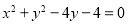 ,双曲线的左、右顶点
,双曲线的左、右顶点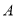 、
、 是该圆与
是该圆与
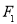 、
、 ,试在“8”字形曲线上求点
,试在“8”字形曲线上求点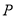 ,使得
,使得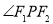 是直角.
是直角.