题目内容
已知函数 处的切线l与直线
处的切线l与直线 垂直,函数
垂直,函数
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若函数 存在单调递减区间,求实数
存在单调递减区间,求实数 的取值范围;
的取值范围;
(Ⅲ)设 是函数
是函数 的两个极值点,若
的两个极值点,若 ,求
,求 的最小值。
的最小值。
(Ⅰ) ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)
;(Ⅲ)
【解析】
试题分析:(Ⅰ)利用求导,将 处的切线的斜率求出,与直线
处的切线的斜率求出,与直线 的斜率乘积为
的斜率乘积为 ,进而求得
,进而求得 的值;(Ⅱ)根据(Ⅰ)得到
的值;(Ⅱ)根据(Ⅰ)得到 的解析式,若函数
的解析式,若函数 存在单调递减区间,必有
存在单调递减区间,必有 在
在 上有解,进而求得
上有解,进而求得 的取值范围;(Ⅲ)根据题意
的取值范围;(Ⅲ)根据题意 的两个根即为
的两个根即为 ,由韦达定理得到
,由韦达定理得到 ,进而
,进而
 ,应换元法进而求得其最小值.
,应换元法进而求得其最小值.
试题解析:(Ⅰ) ,
,
 垂直,
垂直, ,
, (3分)
(3分)
(Ⅱ)
 (5分
(5分
设 ,则
,则 只须
只须
 的取值范围为
的取值范围为 (8分)
(8分)
(Ⅲ)令

 (10分)
(10分)
 ,
,
又

 ,令
,令
 ,
, (12分)
(12分)

故 的最小值为
的最小值为 (14分)
(14分)
考点:1.利用导求切线斜率;2.利用导解决单调递减区间;3.换元法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, ,
, ,D是AB边上的一点,以BD为直径的⊙
,D是AB边上的一点,以BD为直径的⊙ 与AC相切于点E。若BC=6,则DE的长为
与AC相切于点E。若BC=6,则DE的长为 
 ,值域为 ,不等式
,值域为 ,不等式 的解集为 .
的解集为 .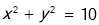 ,
,  内接于此圆,
内接于此圆, 点的坐标
点的坐标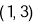 .若
.若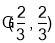 ,则线段
,则线段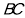 的中点坐标为 ,直线
的中点坐标为 ,直线 ,
,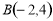 ,
,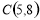 ,若线段
,若线段 和
和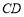 有相同的中垂线,则点
有相同的中垂线,则点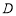 的坐标是
的坐标是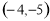 B.
B.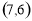 C.
C.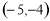 D.
D.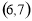
 ,定义
,定义 ,对于任意不小于2的正整数
,对于任意不小于2的正整数 ,设
,设 ,
,
 ,
, 。
。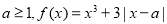 ,若函数
,若函数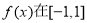 上的最大值和最小值分别记为
上的最大值和最小值分别记为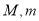 ,则
,则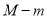 的值为 ( )
的值为 ( )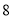 B.
B.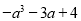 C.
C.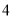 D.
D.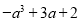
 上点到直线
上点到直线 的距离的最小值称为曲线
的距离的最小值称为曲线 到直线
到直线 的距离等于曲线
的距离等于曲线 到直线
到直线 的距离,则实数
的距离,则实数
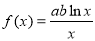 ,
,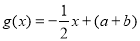 (其中
(其中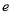 为自然对数的底数,
为自然对数的底数,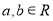 且
且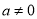 ),曲线
),曲线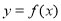 在点
在点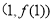 处的切线方程为
处的切线方程为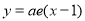 .
.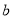 的值;
的值;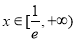 ,
,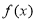 与
与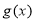 有且只有两个交点,求
有且只有两个交点,求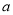 的取值范围.
的取值范围.