��Ŀ����
�ڣ�x2+x+1��n=D
x2n+D
x2n-1+D
x2n-2+��+D
x+D
��n��N����չ��ʽ�У���D
��D
��D
������D
��������ʽ��n��ϵ���У�
������������ʽ��1��ϵ������1��1��1����գ�
����ʽ��2��ϵ������ ��
����ʽ��3��ϵ������ ��
������ʽ��a+b��n��n��N����չ��ʽ�У�ϵ��������������������ʾ������

�ٵ�0��n��4��n��Nʱ�������������������������г�����ʽ��n��ϵ���е��������
�������������������пɵó����ʣ�C
=C
+C
�����Ƶ���������ʽ��n��ϵ����ʾD
��1��k��2n-1��k��N��������֤������
�������ö���ʽϵ�������������ʾD
��
0 n |
1 n |
2 n |
2n-1 n |
2n n |
0 n |
1 n |
2 n |
2n n |
������������ʽ��1��ϵ������1��1��1����գ�
����ʽ��2��ϵ������
����ʽ��3��ϵ������
������ʽ��a+b��n��n��N����չ��ʽ�У�ϵ��������������������ʾ������

�ٵ�0��n��4��n��Nʱ�������������������������г�����ʽ��n��ϵ���е��������
�������������������пɵó����ʣ�C
n n+1 |
n n |
n-1 n |
k+1 n+1 |
�������ö���ʽϵ�������������ʾD
3 n |
���㣺����ʽϵ��������
ר�⣺�ۺ���,����ʽ����
�����������ɣ�x2+x+1��2=x4+x2+1+2x3+2x2+2x=x4+2x3+3x2+2x+1�����2��ϵ���У�ͬ�����ݣ�x2+x+1��3=��x4+2x3+3x2+2x+1����x2+x+1��=x6+3x5+6x4+7x3+6x2+3x+1�����3��ϵ���У�
���٢���ͼ��ʾ����������ʽ��2��ϵ���к�3��ϵ���еĶ��壬�ɵý��ۣ�
����������ʽ��2��ϵ���к�3��ϵ���еĶ��壬�������������ʽ�����ʣ����ö���ʽϵ����ʾ
���٢���ͼ��ʾ����������ʽ��2��ϵ���к�3��ϵ���еĶ��壬�ɵý��ۣ�
����������ʽ��2��ϵ���к�3��ϵ���еĶ��壬�������������ʽ�����ʣ����ö���ʽϵ����ʾ
���
�⣺���ߣ�x2+x+1��2=x4+x2+1+2x3+2x2+2x=x4+2x3+3x2+2x+1��
������ʽ��2��ϵ������1��2��3��2��1��
�ߣ�x2+x+1��3=��x4+2x3+3x2+2x+1����x2+x+1��=x6+3x5+6x4+7x3+6x2+3x+1��
������ʽ��3��ϵ������1��3��6��7��6��3��1��
�����г�������������Ƶı���0��n��4��n��N����
1
1 1 1
1 2 3 2 1
1 3 6 7 6 3 1
1 4 10 16 19 16 10 4 1
��
=
�� 1��k��2 n-1 ����
�����ɣ��ڿɵ�
=1+n-2+
=
��
��
=n-1=
-1��
����
=
��
-
=
-1
n�ֱ�ȡ3��4������n���룬�ۼӿɵ�
-
=
+
+
-��n-2��=
-��n+2����
��
=2��
��
=
-
��
������ʽ��2��ϵ������1��2��3��2��1��
�ߣ�x2+x+1��3=��x4+2x3+3x2+2x+1����x2+x+1��=x6+3x5+6x4+7x3+6x2+3x+1��
������ʽ��3��ϵ������1��3��6��7��6��3��1��
�����г�������������Ƶı���0��n��4��n��N����
1
1 1 1
1 2 3 2 1
1 3 6 7 6 3 1
1 4 10 16 19 16 10 4 1
��
| D | k+1 n+1 |
| D | k-1 n |
| +D | k n |
| +D | k+1 n |
�����ɣ��ڿɵ�
| D | 2 n-1 |
| C | 2 n-1 |
| C | 2 n |
��
| D | 1 n-1 |
| C | 1 n |
����
| D | 3 n |
| D | 1 n-1 |
| +D | 2 n-1 |
| +D | 3 n-1 |
| D | 3 n |
| D | 3 n-1 |
| C | 2 n+1 |
n�ֱ�ȡ3��4������n���룬�ۼӿɵ�
| D | 3 n |
| D | 3 2 |
| C | 2 4 |
| C | 2 5 |
| C | 2 n+1 |
| C | 3 n+2 |
��
| D | 3 2 |
��
| D | 3 n |
| C | 3 n+2 |
| C | 1 n |
������������Ҫ�������ʽ������Ӧ�ã�������ļ��㹫ʽ��Ӧ�ã������е��⣮

��ϰ��ϵ�д�
 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д� ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д� �㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�����Ŀ
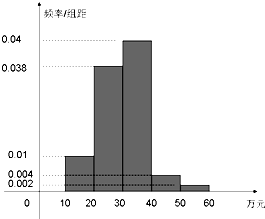 ��ij�е��˴��ѡ���У�������ͳ�Ƹ����˴�������ܻ������Ƶ�ʷֲ�ֱ��ͼ��ͼ�������ܻ�[10��20]��Ԫ����10�ˣ�
��ij�е��˴��ѡ���У�������ͳ�Ƹ����˴�������ܻ������Ƶ�ʷֲ�ֱ��ͼ��ͼ�������ܻ�[10��20]��Ԫ����10�ˣ� ��ͼ����֪P��ԲO��һ�㣬PAΪ ԲO�����ߣ�AΪ�е㣮����PBC����Բ��O����PA=3
��ͼ����֪P��ԲO��һ�㣬PAΪ ԲO�����ߣ�AΪ�е㣮����PBC����Բ��O����PA=3