题目内容
(本小题满分13分)已知抛物线 的焦点为
的焦点为 ,
, 是抛物线上横坐标为4、且位于
是抛物线上横坐标为4、且位于 轴上方的点,
轴上方的点, 到抛物线的准线的距离为5,过
到抛物线的准线的距离为5,过 作
作 垂直于
垂直于 轴,垂足为
轴,垂足为 ,
, 的中点为
的中点为 .
.

(1)求抛物线的方程;
(2)过 作
作 ,垂足为
,垂足为 ,求点
,求点 的坐标.
的坐标.
 的焦点为
的焦点为 ,
, 是抛物线上横坐标为4、且位于
是抛物线上横坐标为4、且位于 轴上方的点,
轴上方的点, 到抛物线的准线的距离为5,过
到抛物线的准线的距离为5,过 作
作 垂直于
垂直于 轴,垂足为
轴,垂足为 ,
, 的中点为
的中点为 .
.
(1)求抛物线的方程;
(2)过
 作
作 ,垂足为
,垂足为 ,求点
,求点 的坐标.
的坐标.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)根据抛物线的标准方程,先写出抛物线的准线方程,进而由抛物线的定义得到
 ,进而可确定
,进而可确定 ,从而可写出抛物线的方程;(2)由(1)先确定
,从而可写出抛物线的方程;(2)由(1)先确定 ,
, ,随之确定
,随之确定 ,进而写出直线
,进而写出直线 的方程,进而由
的方程,进而由 得到
得到 ,进而写出直线
,进而写出直线 的方程,最后联立直线
的方程,最后联立直线 、
、 的方程即可求得交点
的方程即可求得交点 的坐标.
的坐标.试题解析:(1)抛物线
 的准线为
的准线为 ,于量
,于量 ,所以
,所以
∴抛物线方程为

(2)由(1)可得点
 的坐标是
的坐标是 , 由题意得
, 由题意得
又∵
 , ∴
, ∴ ,由
,由 可得
可得
则
 的方程为
的方程为 ,
, 的方程为
的方程为
解方程组
 ,所以
,所以 .
.
练习册系列答案
相关题目
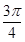 ,直线l1经过点A(3,2)和B(a,-1),且直线l1与直线l垂直,直线l2的方程为2x+by+1=0,且直线l2与直线l1平行,则a+b等于( )
,直线l1经过点A(3,2)和B(a,-1),且直线l1与直线l垂直,直线l2的方程为2x+by+1=0,且直线l2与直线l1平行,则a+b等于( )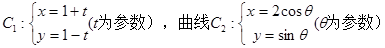 ,若
,若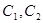 交于A、B两点,则弦长
交于A、B两点,则弦长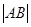 为( )
为( )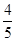 B.
B.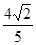 C.
C.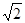 D.4
D.4 ,则动点P的轨迹方程是( )
,则动点P的轨迹方程是( )



 ,过圆心C作直线l交圆于A、B两点,交y轴于点P,若A恰好为线段BP的中点,则直线l的方程为 .
,过圆心C作直线l交圆于A、B两点,交y轴于点P,若A恰好为线段BP的中点,则直线l的方程为 .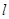 :(2m+1)x+(m+1)y﹣7m﹣4=0恒过一定点P,则点P的坐标为 .
:(2m+1)x+(m+1)y﹣7m﹣4=0恒过一定点P,则点P的坐标为 .