题目内容
(本小题满分12分)
在平面直角坐标系中,有三个点的坐标分别是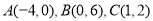 .
.
(1)证明:A,B,C三点不共线;
(2)求过A,B的中点且与直线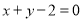 平行的直线方程;
平行的直线方程;
(3)设过C且与AB所在的直线垂直的直线为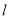 ,求
,求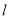 与两坐标轴围成的三角形的面积.
与两坐标轴围成的三角形的面积.
(1)见解析,(2) ,(3)
,(3)
【解析】
试题分析:注意证明平面当中的三点不共线的方法,可以应用两点所在直线的斜率不相等来处理,对应第二问需要知道两直线平行时的条件,应用点斜式方程可得结果,也可应用平行直线系方程的应用,对应第三问,要明确两直线垂直的条件,可以应用点斜式方程,也可应用垂直直线系方程,来求出对应的直线方程,从而找出和坐标轴的交点,得出所得的三角形的面积.
试题解析:(1)∵ , (1分)
, (1分)
 , (2分)
, (2分)
∴ , (3分)
, (3分)
∴ 三点不共线. (4分)
三点不共线. (4分)
(2)∵ 的中点坐标为
的中点坐标为 , (5分)
, (5分)
直线 的斜率
的斜率 , (6分)
, (6分)
所以满足条件的直线方程为 ,即
,即 为所求. (8分)
为所求. (8分)
(3)∵ ,∴与AB所在直线垂直的直线的斜率为
,∴与AB所在直线垂直的直线的斜率为 , (9分)
, (9分)
所以满足条件的直线 的方程为
的方程为 ,即
,即 . (10分)
. (10分)
因为直线 在
在 轴上的截距分别为4和
轴上的截距分别为4和 , (11分)
, (11分)
所以 与两坐标轴围成的三角形的面积为
与两坐标轴围成的三角形的面积为 . (12分)
. (12分)
考点:证明三点不共线的方法,平行直线系,垂直直线系,直线方程的点斜式,三角形的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, ,
, ,则
,则 B.
B. C.
C. D.
D.
 ”是“
”是“ ”的
”的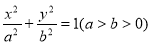 的离心率为
的离心率为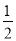 ,其左焦点
,其左焦点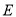 与抛物线
与抛物线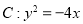 的焦点相同.
的焦点相同.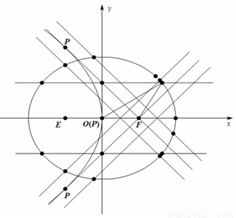
 的直线
的直线 与曲线
与曲线 只有一个交点
只有一个交点 ,则
,则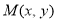 ,使得
,使得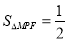 ,若存在,请说明一共有几个点;若不存在,请说明理由.
,若存在,请说明一共有几个点;若不存在,请说明理由. ,
, ,
,
 三点共线,则
三点共线,则 =
= 

 B.
B.
 C.
C.
 D.
D.

 ”是“
”是“ ”( )条件
”( )条件
