题目内容
已知二次函数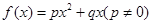 ,其导函数为
,其导函数为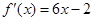 ,数列
,数列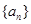 的前
的前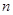 项和为
项和为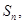 点
点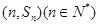 均在函数
均在函数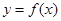 的图像上;.
的图像上;.
(Ⅰ)求数列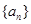 的通项公式;
的通项公式;
(Ⅱ)若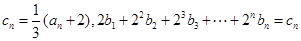 ,求数列
,求数列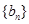 的通项公式;
的通项公式;
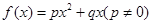 ,其导函数为
,其导函数为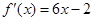 ,数列
,数列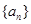 的前
的前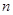 项和为
项和为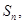 点
点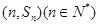 均在函数
均在函数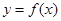 的图像上;.
的图像上;.(Ⅰ)求数列
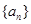 的通项公式;
的通项公式;(Ⅱ)若
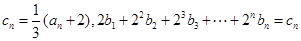 ,求数列
,求数列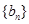 的通项公式;
的通项公式;(Ⅰ)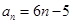 ;(Ⅱ)
;(Ⅱ)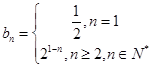 。
。
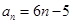 ;(Ⅱ)
;(Ⅱ)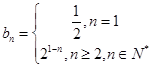 。
。本试题考查了函数与数列的关系,以及数列求和的综合运用。
(1)根据已知条件,二次函数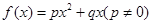 ,则
,则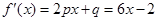
故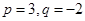 所以
所以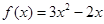 ,点
,点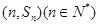 均在函数
均在函数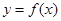 的图像上,
的图像上,
则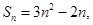 利用通项公式与前n项和的关系式得到通项公式的求解。
利用通项公式与前n项和的关系式得到通项公式的求解。
(2)由(Ⅰ)得,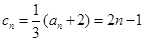 ,
,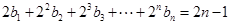 ,利用整体的和式,相减得到通项公式。
,利用整体的和式,相减得到通项公式。
解:(Ⅰ)已知二次函数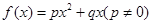 ,则
,则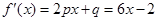
故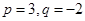 ……………………………2分
……………………………2分
所以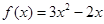 ,点
,点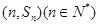 均在函数
均在函数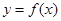 的图像上,
的图像上,
则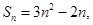 当
当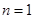 时,
时,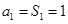 ;当
;当 时,
时, ……5分
……5分
故数列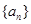 的通项公式:
的通项公式: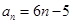 ………………………………6分
………………………………6分
(Ⅱ)由(Ⅰ)得,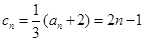 ,
,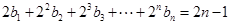 ,
,
当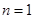 时,
时,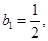 …………………………………7分
…………………………………7分
当 时,
时,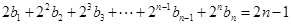
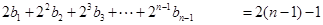
两式相减得: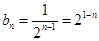 ,……………………………………11分
,……………………………………11分
故数列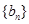 的通项公式:
的通项公式: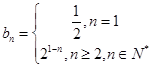 ……………………………12分
……………………………12分
(1)根据已知条件,二次函数
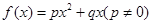 ,则
,则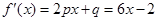
故
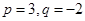 所以
所以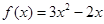 ,点
,点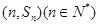 均在函数
均在函数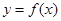 的图像上,
的图像上,则
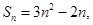 利用通项公式与前n项和的关系式得到通项公式的求解。
利用通项公式与前n项和的关系式得到通项公式的求解。(2)由(Ⅰ)得,
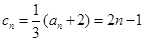 ,
,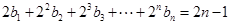 ,利用整体的和式,相减得到通项公式。
,利用整体的和式,相减得到通项公式。解:(Ⅰ)已知二次函数
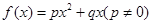 ,则
,则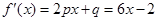
故
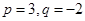 ……………………………2分
……………………………2分所以
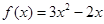 ,点
,点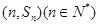 均在函数
均在函数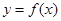 的图像上,
的图像上,则
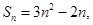 当
当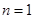 时,
时,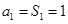 ;当
;当 时,
时, ……5分
……5分故数列
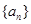 的通项公式:
的通项公式: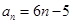 ………………………………6分
………………………………6分(Ⅱ)由(Ⅰ)得,
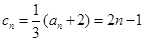 ,
,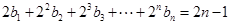 ,
,当
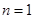 时,
时,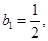 …………………………………7分
…………………………………7分当
 时,
时,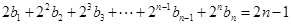
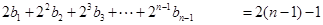
两式相减得:
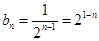 ,……………………………………11分
,……………………………………11分故数列
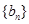 的通项公式:
的通项公式: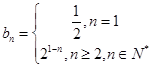 ……………………………12分
……………………………12分
练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
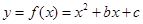 的图象过点(1,13),
的图象过点(1,13),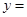
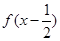 是偶函数.
是偶函数.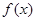 的解析式;
的解析式;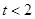 ,
,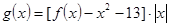 ,求函数
,求函数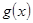 在[
在[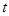 ,2]上的最大值和最小值.
,2]上的最大值和最小值.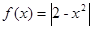 ,若
,若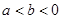 ,且
,且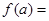
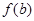 ,则
,则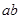 的取值范围是
的取值范围是  ,方程
,方程 的两根
的两根 和
和 满足
满足 .
. 的取值范围;
的取值范围; 与
与 的大小.并说明理由.
的大小.并说明理由.  的值域为
的值域为 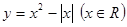 的图像,并指出它的单调区间.
的图像,并指出它的单调区间.
 对任意实数t都有f (3+ t) =" f" (3-t),那么( )
对任意实数t都有f (3+ t) =" f" (3-t),那么( )
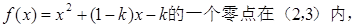 则实数k的取值范围是()
则实数k的取值范围是()