Question

已知平面α∥β,AB、CD为夹在α、β间的异面线段，E、F分别为AB、CD的中点.求证:EF∥α,EF∥β.

Answer 1

分析:要证EF∥α，根据线面平行的判定定理，只需在α内找一条直线与EF平行；或过EF作一平面，使该平面与α平行，据面面平行的性质定理即可证得.

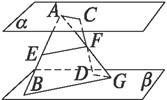
证法一:

连结AF并延长交β于G?.

∵AG∩CD=F,

∴AG、CD确定平面γ，且γ∩α=AC,γ∩β=DG.

∵α∥β,∴AC∥DG.∴∠ACF=∠GDF.

又∠AFC=∠DFG，CF=DF,

∴△ACF≌△GDF.∴AF=FG.

又AE=BE,∴EF∥BG.

∵BGβ,∴EF∥β.

同理,FE∥α.

证法二:∵AB与CD为异面直线,∴ACD.

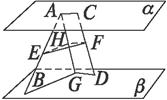
在A、C、D确定的平面内过点A作AG∥CD交β于点G，取AG的中点H，连结AC、HF.

∵α∥β,∴AC∥DG∥FH.

∵DGβ,∴HF∥β.

又∵E为AB的中点,

∴EH∥BG.∴EH∥β.

又EH∩HF=H,∴平面EHF∥β.

∵EF平面EHF,∴EF∥β.同理,EF∥α.