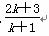题目内容
设矩形ABCD(AB＞AD)的周长为24，把它关于AC折起来，AB折过去后交CD于点P，如图，设AB＝x，求△ADP的面积的最大值，及此时x的值．
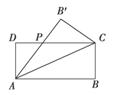
解：∵AB＝x，∴AD＝12－x，
又DP＝PB′，AP＝AB′－PB′＝AB－DP，
即AP＝x－DP，
∴(12－x)2＋PD2＝(x－PD)2，得PD＝12－
，
∵AB＞AD，∴6＜x＜12，
∴△ADP的面积S＝
AD·DP
＝108－6
≤108－6·2
＝108－72
，
当且仅当
，即x＝6时取等号，
∴△ADP面积的最大值为108－72，此时
x＝6.
练习册系列答案
相关题目
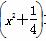＞lgx(x＞0)
≥2(x≠kπ，k∈Z)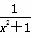
＞1(x∈R)
，求函数y＝4x(3－2x)的最大值；
知x，y都是正实数，且x＋y－3xy＋5＝0，求xy的最小值．
D是由x轴和曲线y＝f(x)及该曲线在点(1,0)处的切线所围成的封闭区域，则z＝x－2y在D上的最大值为________．
．2k＋1 B．2(2k＋1)
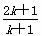D. 