题目内容
已知定义在(-2,2)上的函数f(x)=
连续.
(Ⅰ)求a,b的值;
(Ⅱ)讨论f(x)的单调性;
(Ⅲ)求f(x)的最值.
|
(Ⅰ)求a,b的值;
(Ⅱ)讨论f(x)的单调性;
(Ⅲ)求f(x)的最值.
(I)∵函数f(x)=
连续,
且x≠1时,f(x)=
,得:x=1必是方程:x3+bx2-x-1=0的根,
∴解得b=1,
∴f(x)=
,故a=
=
,
(II)由(I)得f(x)=
=
∵
=x+2+
-2,它可以看成是由函数g(x)=x+
进行图象变换而得,
∵定义域为(-2,2)
∴f(x)的单调性是:在区间(-1,2)上是增函数,在区间(-2,-1)上是减函数,
(III)结合(II)得:f(x)在区间(-1,2)上是增函数,在区间(-2,-1)上是减函数
∴f(x)在x=-1时取得最小值,且f(x)的最小值为:f(-1)=0.
|
且x≠1时,f(x)=
| x 3+bx 2-x-1 |
| (x-1)(x+2) |
∴解得b=1,
∴f(x)=
|
| (1+1) 2 |
| 1+2 |
| 4 |
| 3 |
(II)由(I)得f(x)=
|
| (x+1) 2 |
| x+2 |
∵
| (x+1) 2 |
| x+2 |
| 1 |
| x+2 |
| 1 |
| x |
∵定义域为(-2,2)
∴f(x)的单调性是:在区间(-1,2)上是增函数,在区间(-2,-1)上是减函数,
(III)结合(II)得:f(x)在区间(-1,2)上是增函数,在区间(-2,-1)上是减函数
∴f(x)在x=-1时取得最小值,且f(x)的最小值为:f(-1)=0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
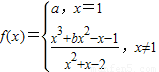 连续.
连续.