题目内容
2.已知定义在R上的奇函数f(x),当x≤0时,f(x)=$\frac{1}{8}$x2+$\frac{1}{2}$x.①求x>0时,f(x)的解析式;
②关于x的方程f(x)=$\frac{1}{2}$a2-1有三个不同的根,求a的取值范围;
③是否存在正实数a,b(a≠b)当x∈[a,b],g(x)=f(x)且g(x)的值域为[$\frac{1}{b}$,$\frac{1}{a}$],若存在,求a,b的值,若不存在,请说明理由.
分析 ①利用函数奇偶性的性质即可求x>0时,f(x)的解析式;
②作出函数f(x)的同学,利用函数与方程的关系进行转化即可求a的取值范围;
③由函数的值域先确定a的取值范围,判断函数的单调性建立方程进行求解即可.
解答 解:①若x>0,则-x<0,
∵当x≤0时,f(x)=$\frac{1}{8}$x2+$\frac{1}{2}$x,
∴当-x<0时,f(-x)=$\frac{1}{8}$x2-$\frac{1}{2}$x,
∵f(x)为奇函数,
∴f(-x)=$\frac{1}{8}$x2-$\frac{1}{2}$x=-f(x),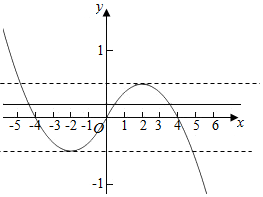
则f(x)=-$\frac{1}{8}$x2+$\frac{1}{2}$x,(x>0);
②作出函数f(x)的图象如图:
当x>0时,f(x)=-$\frac{1}{8}$x2+$\frac{1}{2}$x=-$\frac{1}{8}$(x-2)2+$\frac{1}{2}$,
由图象知若方程f(x)=$\frac{1}{2}$a2-1有三个不同的根,
则-$\frac{1}{2}$<$\frac{1}{2}$a2-1<$\frac{1}{2}$,
即$\frac{1}{2}$<$\frac{1}{2}$a2<$\frac{3}{2}$,
则1<a2<3,即0<a<$\sqrt{3}$或-$\sqrt{3}$<a<-1,
即a的取值范围是0<a<$\sqrt{3}$或-$\sqrt{3}$<a<-1;
③当x>0时,g(x)=f(x)=-$\frac{1}{8}$x2+$\frac{1}{2}$x=-$\frac{1}{8}$(x-2)2+$\frac{1}{2}$,
则函数的对称轴为x=2,函数在(0,2)上为增函数,当x>2时,函数为减函数,
∵g(x)的值域为[$\frac{1}{b}$,$\frac{1}{a}$],
∴$\frac{1}{a}$≤$\frac{1}{2}$,即a≥2,此时函数在[a,b]上为减函数,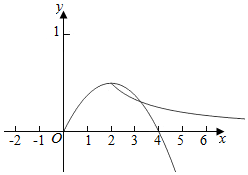
∴$\left\{\begin{array}{l}{g(a)=\frac{1}{a}}\\{g(b)=\frac{1}{b}}\end{array}\right.$,
即a,b是g(x)=$\frac{1}{x}$的两个根,
即-$\frac{1}{8}$(x-2)2+$\frac{1}{2}$=$\frac{1}{x}$,即$\frac{1}{8}$(x-2)2=$\frac{1}{2}$-$\frac{1}{x}$=$\frac{x-2}{2x}$,
即x(x-2)2=4(x-2),
则(x-2)(x2-2x-4)=0,
即x=2或x2-2x-4=0,得x=1$+\sqrt{5}$或x=1-$\sqrt{5}$(舍),
此时a=2,b=1$+\sqrt{5}$.
故存在a=2,b=1$+\sqrt{5}$,使g(x)的值域为[$\frac{1}{b}$,$\frac{1}{a}$].
点评 本题主要考查函数解析式的求解,二次函数的应用以及函数与方程的关系,利用数形结合进行转化是解决本题的关键.综合性较强有一定的难度.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案| A. | c<b<a | B. | b<c<a | C. | c<a<b | D. | a<b<c |

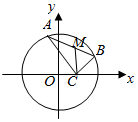 已知点C(1,0),点A,B是⊙O:x2+y2=9上任意两个不同的点,且满足$\overrightarrow{AC}$•$\overrightarrow{BC}$=0,设M为弦AB的中点.
已知点C(1,0),点A,B是⊙O:x2+y2=9上任意两个不同的点,且满足$\overrightarrow{AC}$•$\overrightarrow{BC}$=0,设M为弦AB的中点.