题目内容
 如图,圆锥的顶点是P,O是底面中心.已知PO=
如图,圆锥的顶点是P,O是底面中心.已知PO=| 2 |
(1)计算圆锥的侧面积;
(2)求O到平面APC的距离.
分析:(1)根据题意求出母线的长度,再利用圆锥的侧面积=底面周长×母线长×
,即可求得圆锥的侧面积.
(2)利用VP-AOC=VO-PAC,即可求出O到平面APC的距离.
| 1 |
| 2 |
(2)利用VP-AOC=VO-PAC,即可求出O到平面APC的距离.
解答:解:(1)在Rt△POB中有PO=
,OB=1,
所以PB=
----2’
所以S侧=πrl′=π×1×
=
π,
所以圆锥的侧面积
π.
(2)因为圆O的直径为AB,点C在弧AB上,
所以在Rt△ABC中,AC⊥BC,
又因为AB=2,∠CAB=30°,
所以AC=
.
因为VP-AOC=VO-PAC,即
•S△AOC•PO=
•S△PAC•h,
所以
×(
×1×1×sin120°)×
=
×(
×
2)×h,
解得h=
,
所以O到平面APC的距离为
.
| 2 |
所以PB=
| 3 |
所以S侧=πrl′=π×1×
| 3 |
| 3 |
所以圆锥的侧面积
| 3 |
(2)因为圆O的直径为AB,点C在弧AB上,
所以在Rt△ABC中,AC⊥BC,
又因为AB=2,∠CAB=30°,
所以AC=
| 3 |
因为VP-AOC=VO-PAC,即
| 1 |
| 3 |
| 1 |
| 3 |
所以
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
| ||
| 4 |
| 3 |
解得h=
| ||
| 3 |
所以O到平面APC的距离为
| ||
| 3 |
点评:本题只有考查圆锥侧面积的计算公式与三棱锥的体积公式,以及利用等体积的方法求点到平面的距离,解决此类问题的关键是熟练掌握有关的公式,此题属于中档题.

练习册系列答案
相关题目
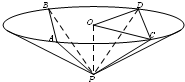 (2013•安徽)如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°,
(2013•安徽)如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°, 如图1,一个密闭圆柱体容器的底部镶嵌了同底的圆锥实心装饰块,容器内盛有a升水.平放在地面,则水面正好过圆锥的顶点P,若将容器倒置如图2,水面也恰过点P.以下命题正确的是( )
如图1,一个密闭圆柱体容器的底部镶嵌了同底的圆锥实心装饰块,容器内盛有a升水.平放在地面,则水面正好过圆锥的顶点P,若将容器倒置如图2,水面也恰过点P.以下命题正确的是( ) 如图,圆锥的顶点是P,O是底面中心.已知
如图,圆锥的顶点是P,O是底面中心.已知 ,圆O的直径AB=2,点C在弧AB上,且∠CAB=30°.
,圆O的直径AB=2,点C在弧AB上,且∠CAB=30°. 如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°,
如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°,