题目内容
若0<x<
,0<y<
,且sinx=xcosy,则( )
| π |
| 2 |
| π |
| 2 |
A、y<
| ||||
B、
| ||||
C、
| ||||
| D、x<y |
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:由于0<x,y<
,可得0<sinx<x<tanx,由sinx=xcosy,可得cosy=
>
=cosx,即y<x,再利用倍角公式可得cosy=
<cos
,即可得出.
| π |
| 2 |
| sinx |
| x |
| sinx |
| tanx |
sin
| ||||
|
| x |
| 2 |
解答:
解:∵0<x,y<
,
∴0<sinx<x<tanx,
又∵sinx=xcosy,
∴cosy=
>
=cosx,
故y<x,
又∵sinx=xcosy,即sin
cos
=
xcosy
∴cosy=
<cos
,
故y>
,
综上所述,
<y<x,
故选:C.
| π |
| 2 |
∴0<sinx<x<tanx,
又∵sinx=xcosy,
∴cosy=
| sinx |
| x |
| sinx |
| tanx |
故y<x,
又∵sinx=xcosy,即sin
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
∴cosy=
sin
| ||||
|
| x |
| 2 |
故y>
| x |
| 2 |
综上所述,
| x |
| 2 |
故选:C.
点评:本题考查了“0<x,y<
,可得0<sinx<x<tanx”性质及其三角函数的单调性、不等式的性质,考查了推理能力与计算能力,属于难题.
| π |
| 2 |

练习册系列答案
相关题目
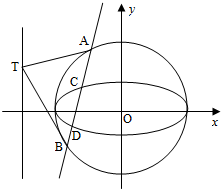 已知椭圆C1的中心在坐标原点,焦点在x轴上,且经过点
已知椭圆C1的中心在坐标原点,焦点在x轴上,且经过点