题目内容
若a,b,c均为实数,且a=x2-2x+
,b=y2-2y+
,c=z2-2z+
,试用反证法证明:a,b,c中至少有一个大于0.
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
考点:反证法与放缩法
专题:证明题,反证法
分析:用反证法,假设a,b,c都小于或等于0,推出a+b+c的值大于0,出现矛盾,从而得到假设不正确,命题得证.
解答:
证明:假设a,b,c都不大于0即a≤0,b≤0,c≤0
根据同向不等式的可加性可得a+b+c≤0①
又a+b+c=x2-2x+
+y2-2y+
+z2-2z+
=(x-1)2+(y-1)2+(z-1)2+
π-3>0与①式矛盾
所以假设不成立,即原命题的结论a,b,c中至少有一个大于0.
根据同向不等式的可加性可得a+b+c≤0①
又a+b+c=x2-2x+
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3 |
| 2 |
所以假设不成立,即原命题的结论a,b,c中至少有一个大于0.
点评:本题的考点是反证法与放缩法,主要考查用反证法证明数学命题,推出矛盾,是解题的关键和难点.

练习册系列答案
相关题目
若0<x<
,0<y<
,且sinx=xcosy,则( )
| π |
| 2 |
| π |
| 2 |
A、y<
| ||||
B、
| ||||
C、
| ||||
| D、x<y |
表面积为4
的正四面体的各个顶点都在同一个球面上,则此球的体积为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
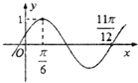 函数f(x)=Asin(ωx+∅)(A>0,ω>0,|∅|<
函数f(x)=Asin(ωx+∅)(A>0,ω>0,|∅|<| π |
| 2 |
| 1 |
| 2 |
A、y=sin(4x+
| ||
B、y=sin(4x+
| ||
C、y=sin(x+
| ||
D、y=sin(x+
|
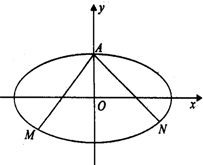 如图已知椭圆
如图已知椭圆