Question

2．已知函数f（x）=$\frac{1}{3}$x³+ax²+b²x+2015（a，b∈R），若从区间[1，3]中任取的一个数a，从区间[0，2]中任取的一个数b，则该函数有两个极值点的概率为（　　）

• A． $\frac{1}{8}$
• B． $\frac{3}{4}$
• C． $\frac{7}{8}$
• D． $\frac{8}{9}$

Answer 1

分析 先求出函数f（x）的导数，得到a＞b，再画出满足条件$\left\{\begin{array}{l}{a＞b}\\{1≤a≤3}\\{0≤b≤2}\end{array}\right.$的平面区域，从而求出满足条件“该函数有两个极值点”的概率．

解答 解：∵函数f（x）=$\frac{1}{3}$x³+ax²+b²x+2015有两个极值点，
∴f′（x）=x²+2ax+b²有两个不同的根，
即判别式△=4a²-4b²＞0，
即当a＞b，该函数有两个极值点，
如下图所示：全部结果所构成的区域为{（a，b）|1≤a≤3，0≤b≤2}（图中矩形所示），其面积为4，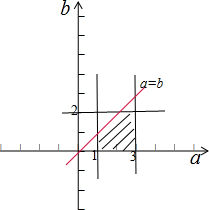
，
满足该函数有两个极值点的区域为：
{（a，b）|1≤a≤3，0≤b≤2，a＞b}（如图阴影所示），其面积为：$\frac{7}{2}$，
∴所求的概率为：$\frac{\frac{7}{2}}{4}$=$\frac{7}{8}$，
故选：C．

点评 本题考查的知识点是几何概型的意义，关键是要找出（a，b）对应图形的面积，及满足条件的点对应的图形的面积；几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P=$\frac{N（A）}{N}$求解．