题目内容
【题目】如图1,已知四边形BCDE为直角梯形,![]() ,
,![]() ,且
,且![]() ,A为BE的中点
,A为BE的中点![]() 将
将![]() 沿AD折到
沿AD折到![]() 位置
位置![]() 如图
如图![]() ,连结PC,PB构成一个四棱锥
,连结PC,PB构成一个四棱锥![]() .
.

![]() Ⅰ
Ⅰ![]() 求证
求证![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() 平面ABCD.
平面ABCD.
![]() 求二面角
求二面角![]() 的大小;
的大小;
![]() 在棱PC上存在点M,满足
在棱PC上存在点M,满足![]() ,使得直线AM与平面PBC所成的角为
,使得直线AM与平面PBC所成的角为![]() ,求
,求![]() 的值.
的值.
【答案】![]() Ⅰ
Ⅰ![]() 详见解析;
详见解析;![]() Ⅱ
Ⅱ![]() ①
①![]() ,②
,②![]() 或
或![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 可以通过已知证明出
可以通过已知证明出![]() 平面PAB,这样就可以证明出
平面PAB,这样就可以证明出![]() ;
;
![]() Ⅱ
Ⅱ![]() 以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,可以求出相应点的坐标,求出平面PBC的法向量为
以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,可以求出相应点的坐标,求出平面PBC的法向量为![]() 、平面PCD的法向量
、平面PCD的法向量![]() ,利用空间向量的数量积,求出二面角
,利用空间向量的数量积,求出二面角![]() 的大小;
的大小;
![]() 求出平面PBC的法向量,利用线面角的公式求出
求出平面PBC的法向量,利用线面角的公式求出![]() 的值.
的值.
证明:![]() Ⅰ
Ⅰ![]() 在图1中,
在图1中,![]() ,
,![]() ,
,

![]() 为平行四边形,
为平行四边形,![]() ,
,
![]() ,
,![]() ,
,
当![]() 沿AD折起时,
沿AD折起时,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
又![]() ,
,![]() 平面PAB,
平面PAB,
又![]() 平面PAB,
平面PAB,![]() .
.
解:![]() Ⅱ
Ⅱ![]() 以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,由于
以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,由于![]() 平面ABCD
平面ABCD
则![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]()
![]() 1,
1,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,
设平面PBC的法向量为![]() y,
y,![]() ,
,
则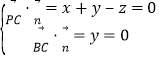 ,取
,取![]() ,得
,得![]() 0,
0,![]() ,
,
设平面PCD的法向量![]() b,
b,![]() ,
,
则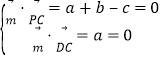 ,取
,取![]() ,得
,得![]() 1,
1,![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,可知为钝角,
,可知为钝角,
则![]() ,
,![]() .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
![]() 设AM与面PBC所成角为
设AM与面PBC所成角为![]() ,
,
![]() 0,
0,![]() ,1,
,1,![]() ,
,![]() ,
,![]() ,
,
平面PBC的法向量![]() 0,
0,![]() ,
,
![]() 直线AM与平面PBC所成的角为
直线AM与平面PBC所成的角为![]() ,
,
![]() ,
,
解得![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】随着手机的普及,大学生迷恋手机的现象非常严重.为了调查双休日大学生使用手机的时间,某机构采用不记名方式随机调查了使用手机时间不超过![]() 小时的
小时的![]() 名大学生,将
名大学生,将![]() 人使用手机的时间分成
人使用手机的时间分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别加以统计,得到下表,根据数据完成下列问题:
分别加以统计,得到下表,根据数据完成下列问题:
使用时间/时 |
|
|
|
|
|
大学生/人 |
|
|
|
|
|

(1)完成频率分布直方图;
(2)根据频率分布直方图估计大学生使用手机的平均时间.


