题目内容
【题目】已知函数![]()
(1)求![]() 的定义域;
的定义域;
(2)判断![]() 的奇偶性并给予证明;
的奇偶性并给予证明;
(3)求关于x的不等式![]() 的解集.
的解集.
【答案】(1)![]() ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
【解析】
(1)根据题意,由函数的分析式分析可得![]() ,解可得x的取值范围,即可得答案;
,解可得x的取值范围,即可得答案;
(2)根据题意,由函数的分析式分析可得![]() ,结合函数的奇偶性的定义分析可得结论;
,结合函数的奇偶性的定义分析可得结论;
(3)根据题意,分![]() 与
与![]() 两种情况讨论,求出不等式的解集,综合即可得答案.
两种情况讨论,求出不等式的解集,综合即可得答案.
解:(1)根据题意,函数![]() ,
,
则有![]() ,解可得
,解可得![]() ,
,
即函数![]() 的定义域为
的定义域为![]() ;
;
(2)首先,定义域关于原点对称,函数![]() ,
,
则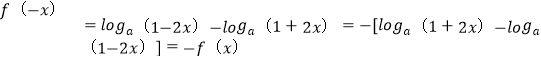
则函数![]() 为奇函数,
为奇函数,
(3)根据题意,![]() 即
即![]() ,
,
当![]() 时,有
时,有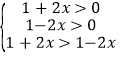 ,解可得
,解可得![]() ,此时不等式的解集为
,此时不等式的解集为![]() ;
;
当![]() 时,有
时,有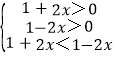 ,解可得
,解可得![]() ,此时不等式的解集为
,此时不等式的解集为![]() ;
;
故当![]() 时,不等式的解集为
时,不等式的解集为![]() ;
;
当![]() 时,不等式的解集为
时,不等式的解集为![]() .
.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近13年的宣传费
(单位:千元)的影响,对近13年的宣传费![]() 和年销售量
和年销售量![]()
![]() 数据作了初步处理,得到散点图及一些统计量的值.
数据作了初步处理,得到散点图及一些统计量的值.

由散点图知,按![]() 建立
建立![]() 关于
关于![]() 的回归方程是合理的.令
的回归方程是合理的.令![]() ,则
,则![]() ,经计算得如下数据:
,经计算得如下数据:
|
|
|
|
|
|
10.15 | 109.94 | 0.16 | -2.10 | 0.21 | 21.22 |
最小二乘法求线性回归方程系数公式
(Ⅰ)根据以上信息,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅱ)已知这种产品的年利润![]() 与
与![]() 的关系为
的关系为![]() .根据(1)的结果,求当年宣传费
.根据(1)的结果,求当年宣传费![]() 时,年利润的预报值是多少?
时,年利润的预报值是多少?