题目内容
已知 ,
, ,
, 在
在 处的切线方程为
处的切线方程为
(Ⅰ)求 的单调区间与极值;
的单调区间与极值;
(Ⅱ)求 的解析式;
的解析式;
(III)当 时,
时,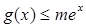 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(Ⅰ)  的增区间为
的增区间为 ,减区间为
,减区间为 ,
, .
.
(Ⅱ)  ,(III)
,(III) .
.
解析试题分析:利用导数求函数的单调性、极值,根据导数的几何意义求函数的解析式;利用导数判定最值的方法求参数的取值范围.
试题解析:(Ⅰ)令 ,得
,得 , 1分
, 1分
∴当 时,
时, ;当
;当 时,
时, .
.
∴ 的增区间为
的增区间为 ,减区间为
,减区间为 ,
, , 3分
, 3分
(Ⅱ)  ,
, ,所以
,所以 .
.
又
∴ ,∴
,∴
所以 6分
6分
(III)当 时,
时, ,令
,令
当 时,
时, 矛盾, 8分
矛盾, 8分
首先证明 在
在 恒成立.
恒成立.
令 ,
, ,故
,故 为
为 上的减函数,
上的减函数, ,故
,故 10分
10分
由(Ⅰ)可知 故当
故当 时,
时,
综上 12分
12分
考点:导数的应用,导数的几何意义,导数最值的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 在
在 的延长线上,
的延长线上, 在
在 的延长线上,且对角线
的延长线上,且对角线 过
过 点.已知
点.已知 米,
米, 米。
米。
 (单位:米),要使花坛
(单位:米),要使花坛 的取值范围;
的取值范围;  (单位:米),则当
(单位:米),则当 ,
,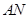 的长度分别是多少时,花坛
的长度分别是多少时,花坛
 的单调区间;
的单调区间; ,求
,求 的取值范围.
的取值范围. .
. 时,求
时,求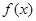 在
在 最小值;
最小值; 的取值范围;
的取值范围; (
( ).
). x
x -ax+(a-1)
-ax+(a-1) ,
, .
. 的单调性;(2)若
的单调性;(2)若 ,设
,设 ,
, ,x
,x

 ,x
,x x
x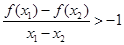 .
. 是实数,函数
是实数,函数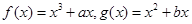 ,
, 和
和 ,分别是
,分别是 的导函数,若
的导函数,若 在区间
在区间 上恒成立,则称
上恒成立,则称 和
和 在区间
在区间 ,若函数
,若函数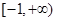 上单调性一致,求实数
上单调性一致,求实数 的取值范围;
的取值范围; 且
且 ,若函数
,若函数 的最大值.
的最大值. .
. 时,求函数
时,求函数 的单调增区间;
的单调增区间; 上的最小值.
上的最小值. (
( ).
). 时,求函数
时,求函数 的极值;
的极值;  ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. )图像上一个最高点坐标为(2,2
)图像上一个最高点坐标为(2,2 ),这个最高点到相邻最低点的图像与x轴交于点(5,0).
),这个最高点到相邻最低点的图像与x轴交于点(5,0).