题目内容
已知函数f(x)= x
x -ax+(a-1)
-ax+(a-1) ,
, .
.
(1)讨论函数 的单调性;(2)若
的单调性;(2)若 ,设
,设 ,
,
(ⅰ)求证g(x)为单调递增函数;
(ⅱ)求证对任意x ,x
,x

 ,x
,x
 x
x ,有
,有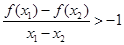 .
.
(1)详见解析;(2)(ⅰ)详见解析;(ⅱ)详见解析.
解析试题分析:(1)先利用导数求出函数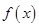 的两个潜在极值点
的两个潜在极值点 与
与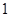 ,由于
,由于 ,可以确定
,可以确定 也在函数的定义域中,然后对
也在函数的定义域中,然后对 与
与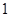 的大小关系分三种情况进行讨论,并求出相应条件下函数
的大小关系分三种情况进行讨论,并求出相应条件下函数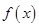 的单调区间;
的单调区间;
(2)(ⅰ)求出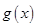 的导数,然后利用导数或
的导数,然后利用导数或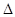 法说明
法说明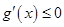 在
在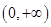 上恒成立,从而证明函数
上恒成立,从而证明函数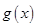 为单调递增函数;(ⅱ)利用(ⅰ)中的结论
为单调递增函数;(ⅱ)利用(ⅰ)中的结论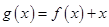 是单调递增函数,并假设
是单调递增函数,并假设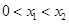 ,由
,由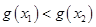 经过变形得到
经过变形得到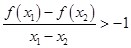 .
.
试题解析:(1) 的定义域为
的定义域为 ,
,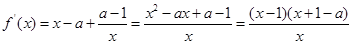 2分
2分
(i)若 即
即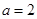 ,则
,则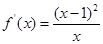 故
故 在
在 单调增加。 3分
单调增加。 3分
(ii)若 ,而
,而 ,故
,故 ,则当
,则当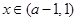 时,
时, ;当
;当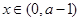 及
及 时,
时, 故
故 在
在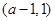 单调减少,在
单调减少,在 单调增加。 5分
单调增加。 5分
(iii)若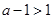 ,即
,即 ,同理可得
,同理可得 在
在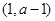 单调减少,在
单调减少,在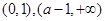 单调增加. 6分
单调增加. 6分
(2) (ⅰ)
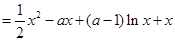
则 7分
7分
由于1<a<5,故 ,即g(x)在(0, +∞)单调增加, 8分
,即g(x)在(0, +∞)单调增加, 8分
(ⅱ)有(ⅰ)知当 时有
时有 ,即
,即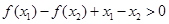 ,
,
故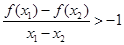 ,当
,当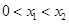 时,有
时,有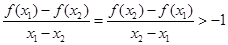 10分
10分
考点:分类讨论、函数的单调性与导数

练习册系列答案
相关题目
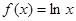 ,若
,若
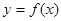 在点
在点 处的切线方程;
处的切线方程; 在区间
在区间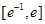 上有两个零点,求实数b的取值范围;
上有两个零点,求实数b的取值范围;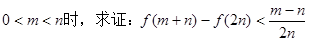
 ,函数
,函数
 在点
在点 处的切线方程; (2)当
处的切线方程; (2)当 时,求
时,求 的最大值.
的最大值. +aln(x-1)(a∈R).
+aln(x-1)(a∈R). <2ln(x-1)<2x-4(x>2);
<2ln(x-1)<2x-4(x>2); +
+ +…+
+…+ <lnn<1+
<lnn<1+ + +
+ + (n∈N*,且n≥2).
(n∈N*,且n≥2).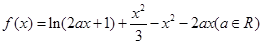
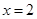 为
为 的极值点,求实数
的极值点,求实数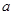 的值;
的值; 在
在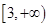 上为增函数,求实数
上为增函数,求实数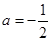 时,方程
时,方程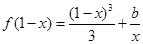 有实根,求实数
有实根,求实数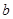 的最大值.
的最大值. ,
, ,
, 在
在 处的切线方程为
处的切线方程为
 的单调区间与极值;
的单调区间与极值; 时,
时,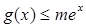 恒成立,求
恒成立,求 的取值范围.
的取值范围.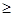 x2在(0,1 )上恒成立,求实数a的取值范围.
x2在(0,1 )上恒成立,求实数a的取值范围. (
(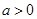 ,
, 为常数)
为常数)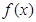 的单调性;
的单调性;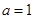 ,证明:当
,证明:当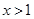 时,
时, .
. .
. 在实数集R上单调递增,求
在实数集R上单调递增,求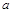 的范围;
的范围; 在
在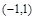 上单调递减.若存在求出
上单调递减.若存在求出